skrypt wzory i prawa z objasnieniami63

124

Przemiany stanu gazu doskonałego

■    W przemianie izoleriuic/ncj gazu doskonałego warunek T - consi j_CS, równoważny warunkowi pV= const lub p\V[ -Pi^2 (prawo Boyle'a . Manune‘a}. W przemianie izoicmicznej /miana energii wewnętrznej jest równa zeru, gdyż temperatura gazu nie zmienia się dU-n CyAT = 0. Gdy gaz pobiera ciepło, lo jest ono całe zużyte na wykonanie przez gaz pracy O - W.

Pracę wykonywaną przez gaz w przemianie izoternneznej obliczamy ze wzoru

Vi

W= [ póV ^v\

Podstawiając ciśnienie p - nRTiV otrzymujemy

W=nRT J ^ =    n-|^

J V    VI

* I

■    Przemiana adiabatyczna jest to proces, podczas którego nie zachodzi wymiana ciepła z otoczeń cm Można to uzyskać poprzez oddzielenie układu od otoczenia dobrymi izolatorami cieplnymi lub jeżeli proces przeprowadzimy dostatecznie szybko.

/ pierwszej zasady termodynamiki AQ-dGid^T wynika, że ponieważ d£ - O ,n» dt'+ćH'=0. Czyli w przemianie adiabatycznej praca wykonywana przez jklać równa est ubytkowi energii wewnętrznej układu, a wiec dłP = - d(/

■    Przyrost energii wewnętrznej układu powoduje wzrost jego temperatury Ten wzrost temperatury powoduje dodatkowy wzrost ciśnienia gazu A więc podczas adiabatycznego sprężania (rozprężania) gazu zmiany ciśnienia są większe niż podczas izolermiczncgo sprężania (rozprężania) gazu (wykres po prawej stronie).

■    7. rów nania adiabaty (równania Pois«ma) dla zmiennychp i V (pY^r -cnnftf' nożna przejść do zmiennych T 1 V Skorzystamy w tym celu z równania Clapcyrona p- *,RT>Y Otrzymujemy pV- nRTV^!V = nRTV ’~^] = const. Stąd !T * = const (stałe występujące w dwóch ostatnich równaniach są oczywiście różne). lak więc równanie adiabaty rriożc być wyrażone poprzez dowolne iwie wielkości spośród p. V. '/'

■    Przemianą połltropową nazwywainy przemianę, podczas której ciepło molowe C (ciepło właściwe c) jest stałe. Równanie poiitropy gazu doskonałego ma postać

pV ⁿ = const, gdzie k -    ; nazywamy W7kładnikicm poiitropy

Wszystkie dotychczas omówione przemiany są szczególnymi przypadkami przemiany poi tropowej. W przemianie izobarycznej C-Cp a więc n = 0. izochoryczncj C = C, czyli n - *, izotcrmicznej n = / Przemiana adiabatyczna również jest przemianą po.itropową dla n = y

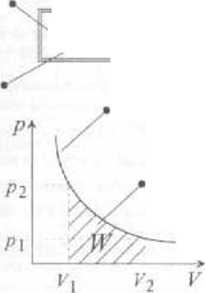
63.3 Przemiana izotermiczna

pV = const

izoterma {T= const)

ciśnienie gazu doskonałego

objętość gazu doskonałego

63.4. Przemiana adiabatyczna

objętość gazu doskonałego

• współczynnik Poissona

równanie Poissona

c^r.ienic gazu doskonałego

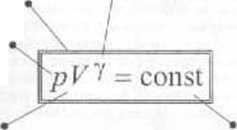
i stała wartość dla danej masy gazu doskonałego

praca w przemianie lzoiermicznej

W= J pdv= nRTin^r

ciepło molowe przy stał\m ciśnieniu

\

~r •

ciepło molowe przy stałej objętości

stała wartość dla danej masy gazu doskonałego

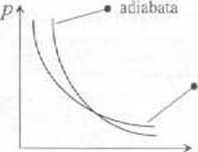
izoterma {T = consri

V