skrypt wzory i prawa z objasnieniami15

28    | Zasady dynamiki klasycznej

■ Zasady dynamiki Newtona są formułowane dla układów inercjalnych Układ inercjalny definiuje pierwsza zasada dynamiki w następujący sposób układ inercjalny to taki układ odniesienia, w którym, jeżeli na ciało nie działa żadna siła lub działające siły równoważą się, to ciało jest w spoczy nku albo porusza się ruchem jednostajnym prostoliniowym. Każdy układ, który porusza się względem danego układu inercjalnego ruchem jednostajnym po linii prostej jest również układem inercjalnym

—^

■ Z drugiej zasady dynamiki wynika, Ze jeżeli siła/’ działająca na ciało (punkt materialny) jest równa zeru. wówczas a 0 . a co za tym idzie, prędkość jest stała. Jest to zgodne z pierwszą zasadą dynamiki.

■ Druga zasada dynamiki jest formułowana dla punktu materialnego Jednakże w praktyce stosujemy ją do ciał o skończonych wymiarach poruszających się ruchem postępowym. Ruchem postępowym nazywamy tak; ruch , w którym wszystkie punkty ciała zakreślają takie same tory' w przestrzeni i mają takie same wartości prędkości "v i przyspieszenia <; w

ABWAW

ruchu

danej chwili czasu i A więc do opisania ruchu ciała wystarczy wybór dowolnego punktu tego ciała Inaczej ruch postępowy ciała można określić jako ruch, w którym dowolny odcinek AB łączący dwa punkty ciała zachowuje stałe ⁴¹ położenie w przestrzeni podczas :iała (patrz rysunek obok) Z określenia ruchu postępowego ciała wynika, że me może ono zmieniać swego kształtu w czasie ruchu t j przynajmniej w przybliżeniu musi się zachowywać jak bryła sztywna

■ Dynamika punktu materialnego najczęściej jest stosowana do opisu ruchu postępowego ciała o skończonych wymiarach Prowadzi to do tego. że w opisach wzorów i komentarzach czasem mówi się o punkcie materialnym, u czasem o ciele

■ Drugą zasadę dynamiki w postaci F = można uogólnić na przypadek relatywistyczny pamiętając o tym . że masa m występująca we wzorze na pęd jest wtenczas funkcją prędkości ( patrz objaśnienie do punktu 53 ).

8. Zasady dynamiki Newtona 8.1 Druga zasada dynamiki

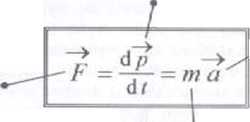
przyspieszenie punktu materialnego d~v _ dr h/-

a -

masa punktu materialnego (cuda) i będąca miarą jego bezwładności

pęd punktu materialnego p = m v

wypadkowa wszystkich sj» działających na punki materialny

druga zasada dynamiki

8.2 Trzecia zasada dynamiki

siła działająca na ciało I ze strony ciała 2 •-

—>    —^    siła działająca na ciało 2

p j2 = — p y |--• ze strony ciała l

trzecia zasada dynamiki dla sił stycznych ciało 2

trzecia zasada dynamiki ^

dla sił centralnych ^/ciało 2

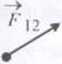
ciało I

—> ^12			^21

ciało 1