skrypt wzory i prawa z objasnieniami48

94

Składanie drgań

■    Reprezentacja drgania harmonicznego przez, obracający się wektor umożliwia w prosty i obrazowy sposób wyprowadzenie wzorów na amplitudę i fazę drgania wypadkowego W tym modelu sens fizyczny przypisujemy jedynie rzutom na oś OX końców wektorów obracających się z częstością kątową to I reprezentujących drgania składowe i drganie wypadkowe).

■    Wyrażenie na amplitudę drgania wypadkowego otrzymujemy z twierdzenia cosinusów dla trójkąta zbudowanego na wektorach o długościach

A, A, i A₂

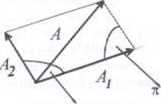
-(<P2-»l)

<P2 — <P I

^2 A~ = A? +A? -24 jj4?cos [* —(<Pj ~9l)]

= a] +Aj +2złj/ł2COS(q>2-<P|)

■    Interesujące jest zbadanie szczególnego przypadku składania drgań. Załóżmy, ze amplitudy drgań składowych są jednakowe tj A,= A, Wówczas amplituda drgania wypadkowego

A = ^2zł|[l -*cos(<P2 — »Pi)] = 2A11cos(^5E!_22J |

Jak widać, gdy różnica faz o; -9i. jest parzystą wielokrotnością p, to drgania sumują się i A 2A,, a dla nieparzystej wielokrotności p. amplituda wypadkow a jest równa zeru.

■    Przedstawiony sposób składania drgań równoległych metodą graficzną ma tę zaletę, że można go uogólnić na składanie dowolnej ilości drgań różniących się między sobą o tę samą wartość fazy początkowej. Ma to duże znaczenie w optyce przy analizie obrazów interferencyjnych i dyfrakcyjnych. Obrazy te powstają jako wynik superpozycji (dodawania się) drgań N wektorów pola elektrycznego, pochodzących od N fal elektromagnetycznych, w danym punkcie ekranu

Drgania harmoniczne

95

46. Składanie drgań 46.1 Składanie drgań równoległych o jednakowych częstościach

x\ |cos(oł +<{>|)    *2 =.42Cos(wł+(o?)

li    I    i

A amplituda    l faza początkowa    l częstość digaii

j pierwszego drgania pierwszego drgania

♦ wychylenie / położenia równowagi w chwili l dla pierwszego drgania

/

wychylenie z położenia równowagi w chwili / dla drgania wypadkowego