skrypt wzory i prawa z objasnieniami21

40

Moc i energia kinetyczna

■ Wychodząc z definicji mocy

P-ŚE ^r dr

i z określenia pracy elementarnej

&w=7&7

otrzymujemy

P= = F v. d/

czyli iloczyn skalamy wektorów siły i prędkości.

■ Załóżmy, Ze na ciało o masie m działa siła wypadkowa F. Wynikiem działania tej siły będzie uzyskanie przez ciało przyspieszenia, zgodnie z II zasada dynamiki Newtona,

rn

Korzystając z powyższego równania wyznaczmy pracę siły wypadkowej

+ c

W = f 7 i? - j m ^d? = \ m? dv = f |d('v ²) =

Załóżmy, że liczby pracę od chwili, w której ciało ma prędkość v,. do chwili, w której uzyskało ono prędkość v₂. czyli.

mvT

^H'=-r-Tⁱ⁼

Wykonana praca równa jest zmianie energii kinetycznej Podkreślmy, że dzieje się tak niezależnie od natury' siły wypadkowej może to być siła grawitacji, ale może byc to również siła napędu rakiety ■ Zwiększanie prędkości ciała (zwiększanie jego energii kinetycznej) wymaga wykonania nad ciałem pracy dodatniej (praca siły pr/yspieszjącej) W' przeciwnym przypadku zmniejszania prędkości (zmniejszania energii kinetycznej), wykonana praca musi być ujemna (praca siły hamującej)

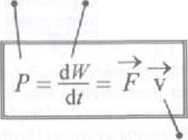
praca wykonywana przez siłę / w czasie od / do r * di

14. Moc

—>

moc siły F w chwili /

prędkość w chwili t jaką posiada ciało, nad którym

siła/*' wykonuje pracę

14.1 Moc średnia

moc średnia siły wykonującej pracę od chwili /| do chwili /i

Y'

r» W

praca wykonana w czasie od chwili /| do chwili /2

Ps =

t₂-t\

15. Energia kinetyczna

w;

r _ wv-^Lk-~

wartość prędkości poruszającego się ciała

energia kinetyczna ciała o masie m

15.1 Związek między pracą a energią kinetyczną

praca niezrównoważonej siły wypadkowej działającej na ciało

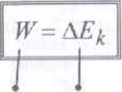
przyrost energii kinetycznej poruszającego się ciała