063 bmp

Przekształcając równania (8.4), otrzymamy warunek równowagi mostka

(8.5)

R, K

skąd

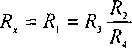
(8.6)

W układzie laboratoryjnym (rys. 8.2) oporniki kołkowe R₂ i Ra służą do wybierania zakresu pomiarowego, zaś równowagę mostka osiąga się przez regulację opornika dekadowego R_z. Prąd galwanomctru magnetoelektrycznego G ograniczony jest opornikiem i? zabezpieczającym przyrząd przed zniszczeniem.

Sposób ręcznego równoważenia mostka jest następujący. Znając rząd wielkości mierzonej rezystancji, dobiera się zakres mostka (stosunek R₂ /Ra),

Po zmniejszeniu czułości galwanometru przez ustawienie maksymalnej wartości rezystancji opornika R włącza się napięcie zasilania mostka U_z. Zerowanie zostaje zapoczątkowane przez zmianę nastawy najwyższej dekady opornika R₂ o jeden stopień (na rys. 8.2 - dekada 9 x 10^J [£2]). Jeżeli na skutek zaistniałej zmiany powiększył się kąt a wychylenia wskazówki galwanometru (wzrost rozrówuoważenia mostka), należy zmieniać położenie pokrętła dekady w kierunku przeciwnym, do momentu uzyskania najmniejszej wartości a. Dalsze równoważenie mostka przy stopniowym jego uczulaniu kolejno przez zwiększanie czułości galwanometru (zmniejszanie wartości R) oraz wzrost wartości napięcia zasilania U_z polega na odpowiedniej zmianie nastaw niższych dekad w celu sprowadzenia wskazówki galwanometru w położenie zerowe. Przy dostatecznie czułym galwanometrze zdarza się. żc mostek nic daje się w pełni zrównoważyć, to znaczy począwszy' od określonej wartości rezystancji nastawionej na oporniku R₃, przy której ot = a_nii_n, zmiana R₃ o wartość AR₂ odpowiadającą skokowi najmniejszej dekady, powoduje wychylenie wskazówki galwanometru po przeciwnej stronie zera skali przyrządu o wartość «i. Rezystancję w gałęzi 3 niezbędną do zrównoważenia mostka należy wtedy wyznaczyć z zależności

R, + A R_i

a

a_l +a_mii

(8.7)

8.2.2. Mostki prądu zmiennego

Zrównoważone mostki prądu zmiennego mają znacznie szersze zastosowanie niż układy stałoprądowc. W metrologii wykorzystuje się je zwłaszcza do wyznaczania impedancji przetworników pojemnościowych oraz indukcyjnych, których elektryczne schematy zastępcze można sprowadzić do szeregowego lub równoległego połączenia dwójników R, C bądź R. L.

Odpowiednio do charakteru mierzonej impedancji ramiona mostków stanowią obwody R, RC, RL_f natomiast w wyniku pomiaru wyznacza się wartości rezystancji R i pojemności C lub indukcyjności L mierzonego elementu.

Dla zrównoważenia mostka zmiennoprądowego f/₀(0 = 0 niezbędna jest regulacja w poszczególnych ramionach amplitud i faz napięć.

Wyrażając impedancje zespolone Z, Ż₄ w postaci sum:

Ż,=R₁₊ jX_l ;

Ż₂ = R_I+jX₂;

gdzie j = V-T - jednostka urojona, otrzymuje się na podstawie zależności (8.1) dwa warunki równowagi mostka prądu zmiennego:

Z₃ = R₃ + JX₃

z₄ = *♦ +

(8.8)

R_iR_A-X_]X~R₂R₃-X₂X_i R_tX_Ą +R,X, = R₂X₃+R_iX₂

(8.9)

Warunki (8.9) wyprowadzono, wykorzystując w (8.1) regułę, że z równości liczb zespolonych wynika równość ich części rzeczywistych i urojonych.

W równaniach (8.8) i (8.9) oznaczono R] + Rą ~ rezystancje ramion mostka, Aj * X₄ -rcaktancje ramion mostka równe: capacitancji 1/toC dla elementów pojemność i owy eh lub induktancji (OL dla elementów indukcyjnych (to - pulsacja),

Zapisując impedancje zespolone w postaci wykładniczej:

Z, = Z,e^M;	Z2 = Z2e^m
Ż3 =Z3e^m-	ŻA = ZAe^m

(8.10)

gdzie Z_L Z₄, tpi tp₄ - kolejno moduły' i argumenty impedancji poszczególnych gałęzi, warunek równowagi sprowadza się do spełnienia równań:

Z, ■ Z_A = Z₂ • Z, <P, + <p₄ = q>, + (p₃

(8.11)

z których bezpośrednio wynika zasada zerowania mostków prądu zmiennego.

Jako przykład omówiony będzie układ mostka Maxw^rella (rys. 8.3) do pomiaru induk-cyjności cewek powietrznych. W jedno z ramion mostka włączona jest cewka o nieznanych wartościach indukcyjności L_x i rezystancji R_x. W pozostałe ramiona włączone są: cewka wzorcowa o parametrach L₂, R₂, oporniki R_2ł Rą o regulowanej rezystancji, potencjometr

Impedancje poszczególnych ramion wynoszą:

Ź[ = R_t + R, + j(aL_x', i = R>;

Z₂ = R₂ + R_n+juL₂, Ż_A = R_A.

127