Image0012 BMP

.2.4. Operator nabla

Podstawowe o|X'racjc różniczkowe analizy wektorowej, a mianowicie gradient, dy-crgcncję i rotacja, można przedstawić w sposób formalny za pomocą operatora wekto-twego zwanego operatorem nabla, bądź, krótko nablą, bądź też operatorem Hamiltona. iperator nabla jest formalnym wektorem i określony jest. wzorem

^V=v_a--+i,^-+vf-;    o-30)

ax ov oz

:st to zatem suma geometryczna trzech operatorów różniczkowania. Mnożąc nablę przez skalar <p, otrzymujemy

dtp 3

a/¹¹-

o r

dę

-h l_t ; = grad <p,

oz

(1.31)

więc gradient skalara. Tworząc iloczyn skalamy nabli przez wektor A, znajdujemy godnie z określeniem iloczynu skalarnego

3A_X vA V-A= ■+■■■-0x 3y

DA.

^y '■    ‘ = div A.

3 z

(1.32)

ryli dywergencję wektora. Natomiast iloczyn wektorowy nabli i wektora A przybiera jstać

V

xA=

(3A₂

\ 8y

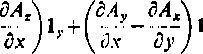
ot A,

tyli równa się rotacji wektora.

Tożsamości wektorowe (1.29) przy zastosowaniu nabli przybierają postać:

VxVp = 0,    V-(VxA) = 0₁    (1.33)

laplasjan

*2 ^2 -2

,    3    3 o

v^a=vv=_;-

coc* 3y~ cs

st sumą trzech operatorów różniczkowania drugiego rzędu.

Laplasjan wektora w układzie współrzędnych prostokątnych określimy za pomocą zoru

0-34)

(1.35)

yli

V²A = V²(M,-tA,A_t+1_sA₌), v²a=i_x v²a_x+1 ‘ V²A_y+1, V^ZA_Z.

iplasjan wektora w układzie współrzędnych prostokątnych jest więc sumą geometryczną plasjanów składowych tego wektora. Tak proste wyrażenie dla laplasjan u wektora jest awdziwę tylko w prostokątnym układzie współrzędnych, a w innych układach otrzy-uje się złożone wzory.

Operator nabla jot określony w układzie współrzędnych prostokątnych, jednakże ruttaty olizj manę przy zastosowaniu tego operatora są prawdziwe w dowolnym ukła-ie współrzędnych.

Operator na lila można stosować przy obliczaniu złożonych operacji wektorowych, u sanie ohlie/cnia sprowadzają się do prostych działań algebry wektorowej. Tak na przykład otrzymuje się

V-(AxB) = B-VxA —A-VxB,\

(1-36)

V x (ęk)~ęSt x A + Vę» x A,    1

V x(V x A) = V(V 'A) —V²A, J

czyli

(137)

div(Ax B) = B-roi A —A • roi B, 1 rot(pA)= protA+grad ętx A,| rot rot A = grad di v A — V²A.    J

1.2.5. Twierdzenie Gaussa-Ostrogradskiego. Twierdzenie Stokesa

Twierdzenie Gaiis.sa-Osirogradskiegu zwane również twierdzeniem Gaussa głosi, że strumień wektora przez powierzchnię zamkniętą jest równy całce objętościowej dywergencji tego wektora w obszarze, którego granicą jest wspomniana powierzchnia, cz.yli

j A-dS= | div Ada.    (1.38)

Sit)    •’

Twierdzenie to można interpretować jako przekształcenie całki powierzchniowej na całkę objętościową.

Pole wektorowe jest polem bezźródiowym lub solenoidalnym w obszarze, gdy dywergencja wektora pola jest równa zeru w każdym punkcie tego obszaru. Na podstawie twierdzenia Gaussa-Ostrogradskiego wnioskujemy, że w polu bezźródiowym strumień wektora pola przez dowolną powierzchnię zamkniętą równa się zeru. Wynik ten można interpretować w ten sposób, że strumień wypływający z pewnego obszaru przez jego granicę równa się strumieniowi wpływającemu do wnętrza tego obszaru.

Pole wektorowe jest źródłowe w obszarze, gdy dywergencja wektora jest różna od zera w tym obszarze lub w jego części. Zgodnie z twierdzeniem Gaussa-Ostrogradskiego wnioskujemy, że strumień wektora poła przez powierzchnię zamkniętą ograniczającą obszar, w którym pole jest źródłowe, nic zanika i jest wielkością różną od zera.

Twierdzenie Stokesa głosi, że całka liniowa wektora pola wzdłuż krzywej zamkniętej równa się strumieniowi rotacji tego wektora przez powierzchnię, której brzegiem jest wspomniana krzyw-a, czyli

Adl = j rot A* dS. '    (1-39)

Clffl

Twierdzenie Stokesa można interpretować jako przekształcenie całki liniowej na całkę powierzchniową.

Pole wektorowe jest polem be żwirowym w obszarze, gdy rotacja wektora jest rnwnu zeru v. każdym punkcie tego obszaru. Zgodnie z twierdzeniem Stokesa, w polu he/.wiro-wym całka liniowa wektora pola wzdłuż, dowolnej krzywej zamkniętej równa się zeru.

Pole wektorowe jest polem iririwiw, gdy rotacja wektora pola jest rożna od zeru w tym obszarze lub w jego części.