Image0018 BMP

1.7. Prawo zachowania ładunku

Na podstawie I prawa Maxwella

„ T SD

rot H=J + —-dt

otrzymujemy

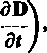
divrotH=div^J + a po uwzględnieniu tożsamości wektorowej (por. wzór 1.29)

mamy

czyli

divrotH=0,

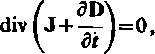
div J_c=0,

(1.84)

(1.85)

gdzie: J_c oznacza gęstość prądu całkowitego (por. p. 1.4).

Otrzymany wynik oznacza, że pole gęstości prądu całkowitego jest polem bezżródło-wym, a linie tego pola są zamknięte. Stwierdzamy zatem, że przepływ prądu całkowitego odbywa się wzdłuż linii zamkniętych. Właściwość tę spotkaliśmy już uprzednio w p. 1.6, przy omawianiu sensu fizycznego prądu przesunięcia.

Z zależności (1.84) otrzymujemy

dD

div J+div — =0, dt

czyli

div J+ — div D=0, dt

a po uwzględnieniu wzoru div D=p, mamy

divJ =

Sp

dt

(1.86)

Oznacza to, że pole gęstości prądu przewodzenia jest źródłowe, a źródłem jego jest zmiana czasowa gęstości ładunku przestrzennego.

W celu uzyskania lepszego obrazu zjawisk, przejdziemy do postaci całkowej. Niech v oznacza obszar w polu elektromagnetycznym, a 5 — granicę tego obszaru; mamy

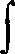
v

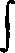
V

div J du= —

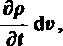
a po zastosowaniu twierdzenia Gaussa-Ostrogradskicgo (por. p. 1.2.5) i po zmianie kolejności operacji różniczkowania oraz całkowania, znajdujemy

*

J’dS — —

dt

j pdo,

czyli

i

S<«)

JdS

dq

dl’

gdzie:

4= Sp do

V

0*7)

0**8)

oznacza ładunek zawarty wewnątrz powierzchni $.

Całka f J-dS przedstawia prąd wypływający z obszaru przez jego granicę. Wzór

S<„)

(1.87) wyraża prawo zachowania ładunku, które głosi, że prąd wypływający z obszaru i’ przez granicę związany jest ze zmianą ładunku zawartego we wnętrzu tego obszaru. Prawo zachowania ładunku obrazuje więc związek prądu przewodzenia z przepływem ładunków.