86271 Ziemniak (3)

Podstawowe wzory algebry i analizy wektorowej

Tożsamości algebraiczne:

A+B=B+A,

A ■ B = B ■ A,

AxB=-BxA,

(A + B)-C = A*C + B- C,

(A + B) x C=Ax C+B x C,

A • (B x C) = B • (C x A) = C • (A x B),

A x(B x C)=(A • C)B —(A-B)C,

(A x B) • (C x D)=(A-C)(B-D)-v(B-C)(A- D).

Tożsamości różniczkowe:

grad (u + v)—grad u + grad v, div(A + B)=divA + divB. rot(A + B) = rotA+rot B, grad (ui?) = u grad o 4- v grad u, div(uA)=udivA-f A*grad u, rot (u A) = u to t A—A x grad u, div(Ax B)=B -rot A—A*rotB, rotrotA = graddivA—V²A, rot grad u = 0, div rotA=0.

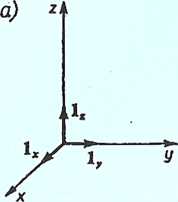
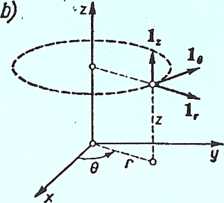
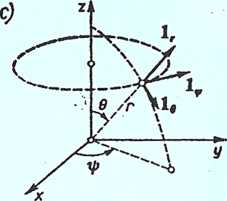
Wersory w układzie współrzędnych prostokątnych (a), w układzie współrzędnych walcowych (b) oraz w układzie współrzędnych kulistych (c)

Tożsamości całkowe:

Twierdzenie Gaussa-Ostrogradskiegó

| A-dS= | divAda ;

S (u)    v

Twierdzenie Stokesa

j A-dI = JrotA-dS;

C(S)    s

Operatory różniczkowe w układzie współrzędnych prostokątnych x, y, zi

du du du gradu = l_J —+ 1,—+1,—,

dA_x dA_y dA_z divA=—+ —+ — , dx dy dz

■ (dA_z dA.\ (dA_x 8A_Z\ YdA_y 3A_X\

*otA = l,^—J + l^— —J+ _z^— —J,

d²u .d²u . d²u Vu=divgrad,=—

V²A=l_x V² A_x + \_yW² A, + l_x V²A_Z.

Operatory różniczkowe w układzie współrzędnych walcowych r, 6, z:

ou 1 du du gradu=l_r^ + I_e——+ 1,—,

1 d(rA_r) 1 dA_e dA_z

divA=-----h--——»

r dr r £d dz

(\ dA_z . rotA=l,|y —-

,    1    -,S

^V“⁼TFr('

(^dAJj±i\+1 ¹ (^{d(rAe) dA}'\

\ć)z dr J ^z r \ dr dQ)

du \    1 d²u .. S²u

W⁺17'

Operatory różniczkowe w układzie współrzędnych kulistych r, 6, y/:

du 1 du    1 du

grad« = l_r-—+ l_fl--—+ 1_—r—r-r~ »

dr r dd ^yrsin0%

1 d(r²A_r) 1 d (A_e sin 0)    T dA+

rsinfl d6 rsinfl dy/

dr

divA=— —t--i r-r——--k

_{w t} 1 rdOVin6) 3A₉1    1 f 1 dA_r d(rAjrI

^f0 rrsin^j_ 86 dy/ J ⁹ r (_sin0 dy/ dr J

_t 1 P(rA.) dA_rl

- ^+lr rL ar de y

^a“V ¹

,    1 d ( ₂ du\ 1 d ( . „

dd J r²sin² 6 dy/'

v    1 ^r +~T ^sm0

r² dr \ 5r / r² sm 0 dQ \