Image0117 BMP

[stawiając e***« cos avr-ł-j sin <ox oraz uwzględniając, że całki zawierające sin out są

ne zeru, gdyż funkcje podcałkowe są nieparzyste względem to, otrzymujemy

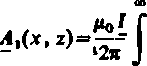
_e~® !*-*!_ _e^_«>(*+*)

o

a)

coscoxdco+

o

viem obie funkcje podcałkowe są parzyste względem co. Przy wykorzystaniu wzoru lanego w p. 12.4, znajdujemy w wyniku

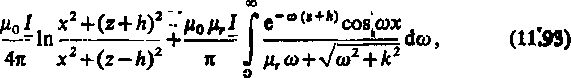
4i(x, z) =

ie: z^O,.

W podobny sposób można wyznaczyć potencjał wektorowy we wnętrzu ściany.

4. METODY WARIACYJNE

1.1. Określenia i zależności podstawowe

Rozwiązanie przybliżone wielu zagadnień brzegowych można wyznaczać za pomocą ;tod wariacyjnych. Na wstępie omówimy krótko podstawowe pojęcia i wzory rachunku riacyjnego.

Funkcjonałem /(«) nazywamy prawo (przepis), które każdej funkcji u z pewnego zbioru przyporządkowuje jedną liczbę I. Zbiór {u} funkcji u, dla których określony jest ikcjonał 7{u) nazywamy dziedziną funkcjonału.

W dalszych rozważaniach rozpatrywać będziemy funkcjonały o ogólnej postaci

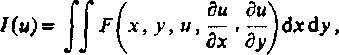
s

(11.94)

reślone dla funkcji dwóch zmiennych u(x, y), przy czym S oznacza jednospójny obszar tski ograniczony krzywą zamkniętą C. Zakładamy, że funkcja u ma ciągłe drugie po-odne.

Warunek konieczny istnienia ekstremum funkcjonału (11.94) wyraża równanie Eulera

dF d 8F 3 dF du tix ou_x cy ću_y

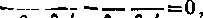
(11.95)

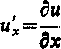
, du oraz = —

' dy

dalszym ciągu zajmiemy się rozwiązaniem zagadnienia Dirichleta dla równania L&-ice’a oraz równania Poissona. Zagadnienie to polega na wyznaczeniu rozwiązania r, y) równania różniczkowego cząstkowego w obszarze S, przy czym u(a,y) jest równe lanej funkcji f(P) na granicy C tego obszaru.

Rozpatrzmy funkcjonał o postaci

(lt.96)

s

przy czym funkcja w(jc, y) jest równa zadanej funkcji /(P) na krzywej brzegowej C obszaru płaskiego S. Mamy tu

i na podstawie równania Eulera (11.95) otrzymujemy

czyli

(11.97)

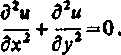
Oznacza to, że funkcja u(x, _>j realizująca extremum funkcjonału (11.96) jest rozwiązaniem zagadnienia Dirichleta dla dwuwymiarowego równania Lapiace’a, tzn. funkcja «(x,y) spełnia równanie Laplace’a (11.97) i podany wyżej warunek brzegowy.

W podobny sposób łatwo udowodnić, że jeżeli funkcja u[x,y) realizuje ekstremum funkcjonału

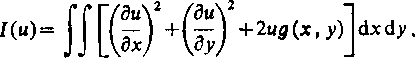
s

(11.98)

przy czym u (*,>■) równa się zadanej funkcji f(P) na granicy obszaru S, to «(x,y) jest rozwiązaniem zagadnienia Dirichleta dla równania Poissona. Funkcja u(x, >-) spełnia wówczas dwuwymiarowe równanie Poissona

(11.99)

przy podanym warunku brzegowym.

W przypadku funkcji w(r, 8) współrzędnych biegunowych r, 8, funkcjonały (11.96) oraz (11.98) przybierają postać

s

s

Bardziej obszerne informacje na temat rachunku wariacyjnego ora2 metod wariacyjnych podane są w pracach [11, 12].