Image0033 BMP

Wyprowmbonc w p. 2.2 wzory ogólne dla potencjału pola elektrostatycznego t dln na-ptęcta w| również prawdziwe dla statycznego pola przepływowego.

Wyprowadzimy równanie dla potencjału V statycznego pola przepływowego przy założeniu, że istnieje ono w jednorodnym Środowisku przewodzącym (y -const). Podstawiając J = yE do zależności divj=0, otrzymujemy

divE=0,

a po podstawieniu wzoru (3.6), mamy

div grad P=0,

czyli

V²K=0.    (3.7),

Potencjał statycznego pola przepływowego spełnia zatem równanie Laplace’a w każdym punkcie obszaru.

3.1.3. Prawo Ohma w postaci wektorowej

Równanie (3.3) wyrażające proporcjonalność wektorów J i E w izotropowym środowisku o konduktywności y, nazywane jest prawem Ohma w postaci wektorowej.

Ma podstawie prawa Ohma w postaci wektorowej można wyprowadzić prawo Ohma wyrażające proporcjonalność napięcia i prądu w oporniku.

Rozpatrzmy odcinek prostoliniowego przewodu walcowego o długości i i o polu S poprzecznego przekroju. Linie poła elektrycznego są równoległe do osi przewodu, wobec czego w jego wnętrzu istnieje pole równomierne. Natężenie pola elektrycznego we wnętrzu przewodu wynosi E=ujl, gdzie u jest napięciem wzdłuż rozpatrywanego odcinka przewodu, a gęstość prądu jest równa ijS, przy czym i oznacza prąd płynący w tym przewodzie.

Podstawiając E=ujł oraz J=ijS do zależności

J=yE,    (3.8)

będącej skalarną postacią wzoru (3.3), otrzymujemy

i u

-_S~^yT

czyli

u=Ri,

gdzie: R=łjyS jest rezystancją odcinka przewodu o długości l, polu S poprzecznego przekroju i konduktywności y.

3.1.4. Prawo Joule'a w postaci różniczkowej

Przy przepływie prądu w środowisku przewodzącym występuje zjawisko przekształcania się energii elektrycznej w ciepło. Zjawisko to raa charakter przestrzenny i zachodzi . w całym obszarze pola przepływowego.

Niech A/^ł oznacza moc przekształcaną w ciepło w obszarze Ai» poła przepływowego. Wielkość

p- lim ~    (3.9)

Au-to Ar

mi/ywa się gęstością objętościową mocy przetwarzanej na ciepło, charakteryzującą rozkład przestrzenny tej wielkości.

Na rysunku 3.1 przedstawiona jest rurka pola przepływowego. Rozpatrzmy odcinek tej rurki między dwiema powierzchniami ekwipotencjaJnymi V oraz V+dV. Niech ÓS oraz. dn oznaczają pole poprzecznego przekroju oraz długość rozpatrywanego odcinka

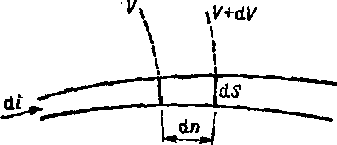
Rys. 3.1. Rurka pola przepływowego

rurki, zaś d» — napięcie wzdłuż tego odcinka. Prąd płynący w rurce wyraża się wzorem ói - J dS. Zgodnie z prawem JouIe’a, moc przetwarzana na ciepło w odcinku rurki jest równa

dP=R(dl)²,

gdzie rezystancja odcinka rurki wynosi

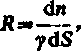
przy czym y jest konduktywnością środowiska. Po wykonaniu elementarnych przekształceń otrzymujemy

(3.10)

gdzie; dr=dS'd« jest objętością rozpatrywanego odcinka rurki. Zgodnie ze wzorem (3.9) gęstość objętościowa mocy wynosi

(3-H)

(3-12)

J²

r

lub

-V2. Warunki brzegowe. Prawo załiamania

Omówimy warunki brzegowe, jakie spełniają wektory J oraz E w polu przepływowym * punktach powierzchni granicznej dwóch środowisk.

Obliczając prąd, czyli strumień wektora J przez powierzchnię walcową (rys. 2.4),