Image0020 BMP

2.2. Potencjał i napięcie 2.2.1. Potencjał pola elektrostatycznego

Ze wzoru

rotE=0 lub $E'dl=0

c

wynika, że pole elektrostatyczne jest polem bezwirowym. W polu bezwirowym można określić funkcję skalarną zwaną potencjałem, która w pełni opisuje to pole.

Rozpatrzmy funkcję skalarną V, określoną w każdym punkcie obszaru, w którym, istnieje pole elektrostatyczne. Funkcja ta zależy od współrzędnych punktu pola, wobec czego dla prostokątnego układu współrzędnych mamy V(x, y, 2). Funkcja ta nazywa się potencjałem elektrycznym, skalarnym potencjałem elektrycznym lub wprost potencjałem. Na podstawie tożsamości wektorowej (por, wzór 1,29)

rot grad F=0,

można przyjąć

E- +grad V,

bowiem spełnione jest równanie rot E=0. W teorii pola elektrostatycznego przyjmuje się

E= —grad F,    (2.9)

a więc wektor E skierowany jest w stronę malejącą potencjałów (por. p. 1.2.1).

Składowe natężenia E pola elektrycznego w układzie współrzędnych prostokątnych wyrażają się wzorami:

wobec czego

dV

dx

E_y

dV dy ’

dv

dz

E

dV _dV dV dx ^x dy ** 8z ¹

(2.10)

(2.11)

Wyrażenia (2.10) oraz (2.11) przedstawiają natężenie pola elektrycznego w zależności od potencjału. Składową wektora E w kierunku osi I przedstawia wzór

(2.12)

dV

dr

dV

gdzie: — oznacza pochodną kierunkową potencjału V w kierunku osi /. di

Przyrost potencjału wzdłuż wektora elementarnego dl wynosi zatem

dF=*—E₍dl*= —Ecosad/,

gdzie: a jest kątem między wektorami E i dl, czyli

d K = — E ■ dl.    (2.13)

Przypuśćmy, że w punkcie N₀ potencjał równy jest zeru, czyli F_No=0; punkt N₀ jest punktem odniesienia dla potencjału. Całkując wyrażenie (2.13) wzdłuż krzywej łączącej

dowolny punki P o potencjale l‘_r i punktem N_VI znajdujemy potencjał w punkcie P

N_u

= | E*dl.    (2.14)

Potencjał w punkcie P pola równa się całce liniowej wektora E natężenia pola elektrycznego wzdłuż krzywej łączącej punkt P z punktem JV₀, w którym potencjał równy jest zeru. Należy przy tym zaznaczyć, że potencjał zerowy przypisuje się często punktowi w nieskończoności lub punktom położonym na powierzchni ziemi.

2.2.2. Napięcie w polu elektrostatycznym

Napięcie u_AB między punktem A a punktem B w polu elektrostatycznym wyraża się wzorem (por. p. 1.4)

U Au

li

jE-dl.

A

(2.15)

Na podstawie wzorów (2.14) i (2.15) stwierdzamy zatem, że potencjał w punkcie P pola elektrostatycznego równa się napięciu między tym punktem a punktem odniesienia, w klóryin potencjał równy jest zeru.

Rozpatrzmy krzywą zamkniętą zawierającą linię łączącą punkty A, B w polu elektro-statyc/.nym oraz punkt N_a, w którym potencjał jest równy zeru (rys. 2.2). Zgodnie z dru-

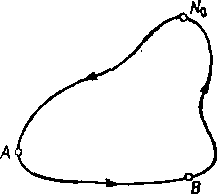
Rys. 2,2. Krzywa zamknięta w polu elektrostatycznym

gim wzorem (2.1) mamy

B    Na    A

| E■ dl + jE'dl+ J E-dl=0,

A    B    N₀

n iiąd

B    No    Nq

JE-dl- JE-dl- |E• dl,

czyli

*am = Va~Vb-

(2.16)

O/nuc/a to, że napięcie między dwoma punktami w polu elektrostatycznym równa się różnicy potencjałów w tych punktach i nie zależy od postaci linii łączącej te punkty ze sobą.