Image0063 BMP

objętości, czyli

w

o

(6.42)

Można wykazać, że wzór (6.42) ma charakter ogólny.

Jeżeli środowisko jest dia- lub paramagnetyczne, to przenikalność magnetyczna ji~ ■ eonst, wobec czego ze wzoru B=fiH wynika, że dB—fidH, czyli

u

= /r J HdH=inH².

0

(6.43)

Wykorzystując wyrażenie B=fiH, otrzymujemy inną postać wzoru na gęstość energii polu magnetycznego, a mianowicie

,    B*

(6.44)

I nrrgia pola magnetycznego zawarta w obszarze o pola magnetycznego wynosi

(6.45)

(idy pole magnetyczne istnieje w środowisku ferromagnetycznym, wówczas całka wklepująca we wzorze (6.43) nie daje się obliczyć w ten sposób jak poprzednio, gdyż przrmkulność magnetyczna pi jest wielkością zmienną, zależną od stanu magnetycznego iiodowjska. Łatwo sprawdzić, że w przypadku ciuła ferromagnetycznego uprzednio nie

B

magnesowanego (bez tzw. przeszłości magnetycznej) całka J ffdB przedstawia zakresko~

0

w»ne na rys. 6.12 pole między krzywą magnesowania a osią rzędnych 0£.

0

Rys. 6.12. Krzywa magnesowania

H

Nn podstawie poprzednich rozważań można łatwo obliczyć energię fV_m zawartą w polu magnetycznym cewki, w której uzwojeniu płynie prąd i. Strumień skojarzony cewki wyraża .się wzorem y—Li, przy czym L jest indukcyjnością własną cewki. Przyjmując, że w otoczeniu cewki nie ma żadnych ciał ferromagnetycznych, mamy L—const, wobec i/cgo dy/ ---Ldi. Na podstawie wzoru (6.40) otrzymujemy

0

(6.46)

Wielkość W_m przedstawioną powyższym wzorem nazywamy energią cewki.

6.5. Obliczanie indukcyjności własnej i wzajemnej 6.5.1. Wzór ogólny dla inilukcyjności wzajemnej

Rysunek 6.13 przedstawia dwa obwody 1,2 o liczbie zwojów odpowiednio równej z, oraz z_lt przewodzące prądy rj, i₂. Niech //=const oznacza przenikalność magnetyczną Modowiska.

Przypuśćmy, że i₂ =0, wobec czego pole magnetyczne wytwarzane jest tylko przez prąd i, w obwodzie 7. Na podstawie wzoru (4.27), strumień skojarzony obwodu 2 można przedstawić w postaci

¥21=2-1 j>A-d!₂,    (6.47)'

Ci

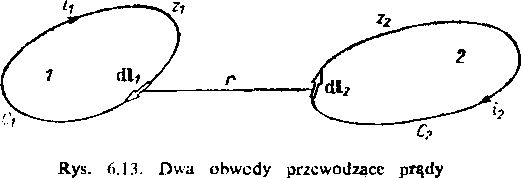
gdzie potencja! wektorowy wyraża się wzorem (por. p. 4.3.2):

_{A =} i ^dli 4jc

c.

(6.48)

przy czym obwód 1 zastąpiono cienkim przewodem wzdłuż krzywej Cj. Po podstawieniu wzoru (6.48) do zależności (6.47), otrzymujemy

(6.49)

fiz_x z₂ ij f f dlj -dlj

Cl Cl

a stąd indukcyjność wzajemna (por. wzór 6.25) ma postać

y/₂\ P^zi ^z2 fX dlj-dl₂

M₂₁=—

4it

Cj Ct

(6.50)

Obecnie założymy, żg /, =0, wobec czego pole magnetyczne wytworzone jest przez prąd i₂ w obwodzie 2. W podobny sposób można udowodnić, że

W,7 =    =

^12 /tZi Z 2

4jc

c_t c₂

f dl_t - dl.

(6.51)

Zmieniając kolejność całkowań w powyższym wzorze, otrzymujemy zależność (6.5(1), wobec czego

(6.52)

M₁₂ = M₂₁.