086 3

16S

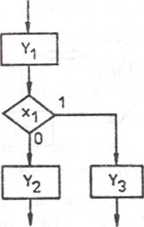
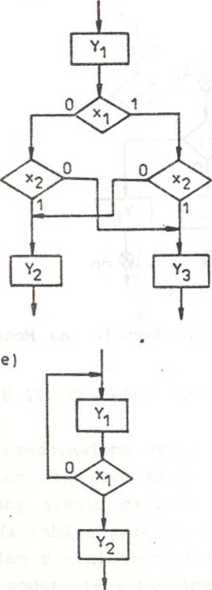
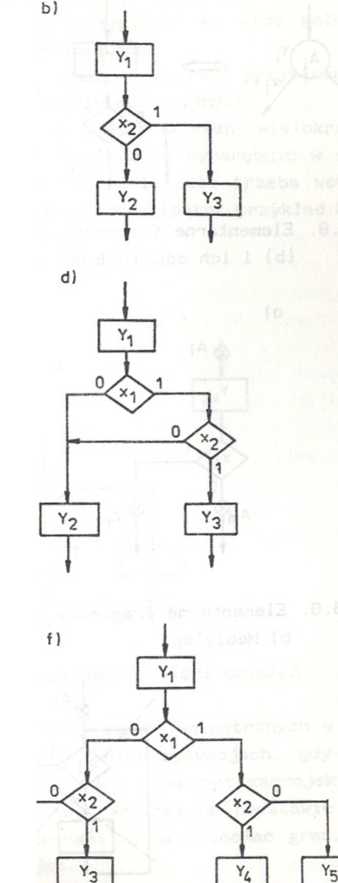
oraz sieci działań. Można wykazać, że istnieje pełna oapowiedniość miedzy tymi dwoma formami opisu; poszczególnym fragmentom grafu (po ich ewentualnych przekształceniach, których przykłady przedstawiają rys. 6.2 i 6.1) można przypisać odpowiednie fragmenty sieci działań i w ten sposób opisać siecią działań dowolny układ sekwencyjny. Na rys. 6.7 przedstawiono fragmenty sieci działań odpowiadające przekształconym fragmentom grafu z rys. 6.2 i 6.1. Założono przy tym, że poszczególnym stanom wewnętrznym A. z rys. 6.2 i 6.1 odpowiadają stany wyjść Y. (graf typu Moore'a). Na rys. 6.8 pokazano zaś elementarne fragmenty grafów typu Moore'a oraz Mealy'ego i ich odpowiedniki w sieci działań.

Podsumowując, stwierdzamy, że opis układu w postaci sieci działań można uzyskać w dwojaki sposób:

-    bezpośrednio na podstawie opisu słownego - w przypadku układów, które ze swej natury spełniają warunek badania co najwyżej jednego sygnału wejściowego w jednym takcie pracy (patrz przykład z rys. 6.5),

-    na podstawie grafu (po jego ewentualnych przekszałceniacn) - w przypadku wszystkich pozostałych układów sekwencyjnych.

Jak już wcześniej stwierdzono, we wszystkich przedstawionych dalej metacacn projektowania układów sterujących, niezbędne jest określenie stanów wewnętrznych w sieci działań. Dla dowolnej sieci działań można to zawsze zrobić dwojako: w wersji Moore’a albo w wersji Mealy'ego. Ogólne zasady nanoszenia stanów wewnętrznych (oznaczanych symbolami (x) w sieci działań są następujące:

1.    Fragmenty sieci między znakami © muszą odpowiadać fragmentom

według rys. 6.9 a (wersja Moore’a) albo według rys. 6.9 b (wersja

Meaiy’ego). Stany , A_m> A_n> w zależności od sytuacji, mogą być

tymi samymi bądź różnymi stanami. Fragmenty sieci z rys. 6.9 mogą

być również zdegenerowane, tzn. dla wersji Moore'a może zostać

opuszczone badanie warunku x. albo operacja Y. ; dla wersji

J    ^K

Mealy ego może nie występować Y^ bądź Yj itp.

2.    Żadna pętla w sieci działań nie może przebiegać przez pusty zbiór stanów (np. rys. 6.10 pokazuje nieprawidłową pętlę).

3.    W celu spełnienia warunków 1 i 2 trzeba niekiedy trochę zmienić sieć działań, np. wstawić operacje puste Yq i ewentualnie powtórzyć badanie pewnych warunków (patrz przykład 6.1- rys. 6. 14 w rozdz. 6.3.1)

Z powyższych ogólnych zasad wynikają następujące szczegółowe wn i osk i:

c)

n n f

^Rys. 6.7. Fragmenty sieci działań fragmentom grafu z rys. 6.2 I

odpowiadające przekształconym + e) i rys. 6.1 (f)