82810 MF dodatekA03

248 Podstawy matematyczne Aneks A

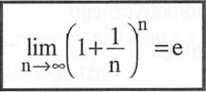
A(1.12)

Można wykazać, że leżeli lim a_n =0 i a_n *0 , to

lim (l+a_n)^a" =e

A(1.13)

Rozważmy ciąg liczbowy {a_n} oraz ciąg

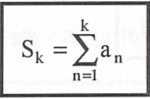
dla k=1,2,3

A(1.14)

Granicę S ciągu {S_k} sum częściowych ciągu { a_n} nazywamy szeregiem liczbowym o wyrazie ogólnym a_n i oznaczamy symbolem

s=f>„    (1.15)

n=l

Jeżeli istnieje granica

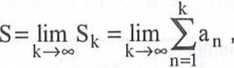
to szereg liczbowy nazywamy zbieżnym, w przeciwnym przypadku szereg ten nazywamy rozbieżnym.

k

Należy pamiętać, że suma skończona ^a_n zawsze istnieje i nie zależy od kolejno-

n=l

oo

ści dodawania, natomiast suma nieskończona ^a_n nie zawsze istnieje i w pew-

n=l

nych przypadkach zależy od kolejności dodawania.