3784490587

193

Ocena możliwości kompensacji niepożądanych,.

Można wykazać, że minimalizacja funkcjonału

<*(i Ą)

2

l₃²(0,t)

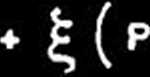
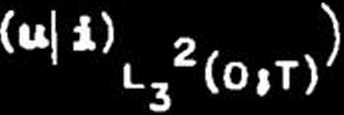
np. metodę nieoznaczonego, czynnika Lagrange’a [io], przy ograniczeniu równościowym stwierdzajęcym, że moc czynna dostarczona do odbiornika powinna być stała i równa wartości zadanej, prowadzi do wyróżnienia tzw. składowej czynnej prędu odbiornika (i), która minimalizuje straty mocy czynnej na symetrycznym doprowadzeniu do odbiornika. (Zakłada się, że przewód zerowy z rys. 1 ma zerowę rezystancję). Składowa ta określona jest wzorem

OO

_ai (t) -Y²' ^{Re    Gu}*h ^exPJ^ht*** ot e {a,b,cj , h 6N (8)

h-1

gdzie i

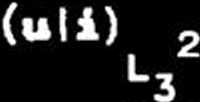
(OjT)

L₃²(°|T)

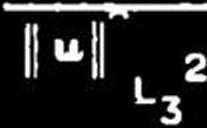
(0|T)

2

Korzystajęc z bazy trygonometrycznej w przestrzeni l_₃ (OjT) pręd odbiornika (i) można rozłożyć na trzy ortogonalne składowe:

- składowa czynna

OO

_ai_A(t) - Y2ⁿ Re 2 ^GU*h ^e*PJ^hu*'    ⁽¹°)

hml

- składowa reaktancyjna

_ri (t) « Y2^{1 R}®    'y [ JB _h U„_h expjhtut,    (li)

h-1 -a

składowa rozrzutu (rozproszenia)

_w e

i (<) ■ Y? »• £]    ‘ ^G<W^ush ^ex«^{hu,    <12}>

h-1    £-a ^r

Jeżeli zdefinioweć wielkości G_h i P_h, tak Jak to uczyniono w pracach

H. W. M