img149
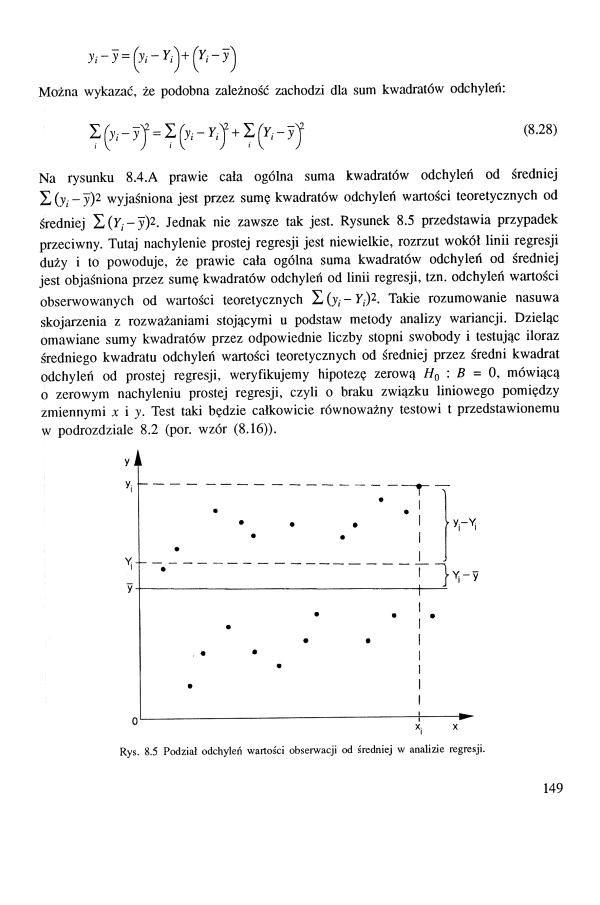
Można wykazać, że podobna zależność zachodzi dla sum kwadratów odchyleń:
(8.28)
Na rysunku 8.4.A prawie cała ogólna suma kwadratów odchyleń od średniej X (y, - y)2 wyjaśniona jest przez sumę kwadratów odchyleń wartości teoretycznych od średniej X(T1--y)2. Jednak nic zawsze tak jest. Rysunek 8.5 przedstawia przypadek przeciwny. Tutaj nachylenie prostej regresji jest niewielkie, rozrzut wokół linii regresji duży i to powoduje, że prawie cała ogólna suma kwadratów odchyleń od średniej jest objaśniona przez sumę kwadratów odchyleń od linii regresji, tzn. odchyleń wartości obserwowanych od wartości teoretycznych X (y, - T,)2. Takie rozumowanie nasuwa skojarzenia z rozważaniami stojącymi u podstaw metody analizy wariancji. Dzieląc omawiane sumy kwadratów przez odpowiednie liczby stopni swobody i testując iloraz średniego kwadratu odchyleń wartości teoretycznych od średniej przez średni kwadrat odchyleń od prostej regresji, weryfikujemy hipotezę zerową //0 : B = 0, mówiącą o zerowym nachyleniu prostej regresji, czyli o braku związku liniowego pomiędzy zmiennymi x i y. Test taki będzie całkowicie równoważny testowi t przedstawionemu w podrozdziale 8.2 (por. wzór (8.16)).
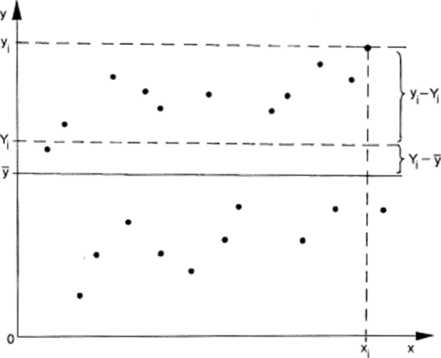
Rys. 8.5 Podział odchyleń wartości obserwacji od średniej w analizie regresji.
149
Wyszukiwarka
Podobne podstrony:
img149 Można wykazać, że podobna zależność zachodzi dla sum kwadratów odchyleń: (8.28) Na rysunku 8.
112 15-16 lat, ale można przypuszczać, że podobne relacje zachodzą także w ciągu kilku następnych la
2 W ogólności:lz = J (x2 + y2)dm = J p(x2 + y2)dV Podobnie można wyznaczyć dla osi Ox i Oy. Można wy
skanuj0138 (11) Rys. 2.13. C„ i dCn/dn jako funkcja n dla foremnych schematów koordynacyjnych. Można
W jaki sposób można wykazać, że ten poziom jest poziomem podstawowym? Wykazano to dla pewnych takson
1 2 Można wykazać, że wymiary zewnętrzne (gabarytowe) pozostałych przekladr 8 i ni będą większe niż
1 2 Można wykazać, że wymiary zewnętrzne (gabarytowe) pozostałych przekladr 8 i ni będą większe niż
1.2: Magnetyczny „pies na smyczy” Cel: wykazanie, że oddziaływanie magnetyczne zachodzi na
65538 slajd11 ) odchylcie Można wykazać, że obserwowane na ekranie oscyloskopu (rys, H wiązki elektr
82810 MF dodatekA�03 248 Podstawy matematyczne Aneks A A(1.12) Można wykazać, że leżeli lim an
Załóżmy teraz, że badane twierdzenie zachodzi dla jakiegoś n = k: 1 + 2 + ...+ * = *(* + 1) Chcemy n
skany003 napięciach polaryzujących złącze w kierunku przewodzenia (0<uD<4Ur). Można wykazać, ż
086 3 16S oraz sieci działań. Można wykazać, że istnieje pełna oapowiedniość miedzy tymi dwoma forma
1 2 Można wykazać, że wymiary zewnętrzne (gabarytowe) pozostałych przekladr 8 • ni będą większe niż
więcej podobnych podstron