01

ramkę 8. W mechanizmie tym ruch obrotowy tarczy 6 zamieniany jest na ruch posuwisto-zwrotny ramki 8 w prowadnicy 2. Tarcza 6 pełni rolę korby (rys. 15.7a), natomiast ramka pity rolę suwaka. Ogniwem wejściowym jest korba, a suwak ogniwem wyjściowym. W celu doświadczalnego pomiaru wielkości kinematycznych ogniwa wyjściowego na ramce pity zamocowano bezwładnościowy czujnik przyśpieszeń 9.

mm

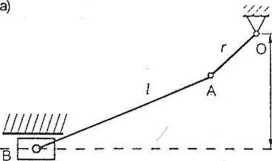
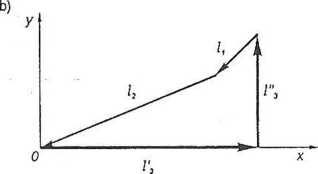
Rys. 15.7

15.5. PRZEBIEG ĆWICZENIA ® Zapoznać się z rysunkiem analizowanego mechanizmu.

•    Zbudować model kinematyczny wybranego mechanizmu.

® Wyznaczyć parametry modelu.

® Napisać algorytm programu do analizy kinematycznej.

® Przeprowadzić analizę kinematyczną mechanizmu.

•    Przeanalizować przebiegi prędkości ru? i a>4 oraz cpj i lub prędkości a>/ i \'u oraz <pi i 5 w zależności od rozpatrywanego mechanizmu.

« Przeprowadzić obliczenia dla innej prędkości 002 lub co\ w zależności od mechanizmu.

•    Przeprowadzić analizę wyników'.

15.6. ZAKRES SPRAWOZDANIA

Sprawozdanie powinno zawierać:

» cel ćwiczenia,

•    wykorzystywane zależności,

® wykresy prędkości i przyspieszeń członów mechanizmu,

•    analizę otrzymanych wyników' i wnioski.

16. POMIAR MOMENTU BEZWŁADNOŚCI BRYŁ SZTYWNYCH ZA POMOCĄ WAHADŁA SKRĘTNEGO

16.1. CEL ĆWICZENIA

Celem ćwiczenia jest zbadanie elipsoidy bezwładności bryły sztywnej za pomocą wahadła skrętnego.

16.2. OBOWIĄZUJĄCY ZAKRES WIEDZY

Student przed przystąpieniem do ćwiczenia powinien znać następujące zagadnienia: ® Momenty bezwładności bryły sztywnej. Elipsoida bezwładności.

• Drgania skrętne. Równanie ruchu drgań skrętnych.

16.3. WSTĘP TEORETYCZNY

Momentem bezwładności bryły sztywnej względem określonej osi obrotu nazywamy wielkość:

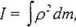
(16.1)

gdzie:    dm - element masy ciała,

p - odległość tego ciała od osi obrotu.

Obliczmy moment bezwładności pewnej bryły względem osi obrotu OA przechodzącej przez początek prostokątnego układu odniesienia Qxyz i tworzącej z osiami tego układu kąty a, /?, y (rys. 16.1).

Rozłóżmy wektor wodzący r elementu masy na składową 7 wzdłuż osi OA i składową p prostopadłą do niej.

Podstawiając otrzymaną wartość p do (16.1) otrzymujemy:

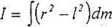
(16.2)

- 141 -