054 055

54

sta, otrzymując minimalną NFS funkcji. Poszczególna impllkanty wypisujemy natychmiast patrząc na daną grupę Jedynek, są to bowiem iloczyny zmień-, nych odpowiadających,zgodnie z (1.10) tym cyfrom w opisie tabeli, które się nie zmieniają przy przebiegnięciu wszystkich Jedynek w obrębie grupy.

Przedstawione na rys. 2.6 przykłady ilustrują podaną metodę. W przykładzie b) nie uwzględniono pary Jedynek odpowiadającej zbędnemu lmpllkan-towi prostemu x₂*j. Istnieje też druga postać minimalna, dla której zbędnym Jest lmplikant    - porównaj z przykładem 2.2 (c.d.). W przykładzie

d) również Istnieje druga postać minimalną wynikająca z zastąpienia składnika    przez składnik    W przykładzie e) zwróćmy uwagę na czwór

kę powstałą z Jedynek leżących~na rogach tablicy. W f) zaistniał interesujący przypadek eliminacji zbędnego lmplikantu XgX₄ - porównaj z przykładem 2.4.

Dotąd mówiliśmy tylko o metodzie tablic Kar na ug ha w zastosowaniu do uzyskiwania minimalnej postaci funkcji Jako sumy implikantów prostych. Wszystkie zasady tworzenia grup 2* Jedynkowych oraz eliminacji zbędnych implikantów obowiązują także dla implicentów z tym, że wtedyj 1° tworzy się grupy zer, 2° odpowiadające utworzonym grupom implicenty wypisujemy Jako sumy zmiennych według przyporządkowania (1.14).

Ha rys. 2.9 przedstawiono kilka przykładów minimalizacji funkcji do HPI.

A)

*1*1

\ M H H W

	obi	0

f ■ (*j * *jX*| ♦ * jX*|^ł *})

M*i

i)

w w « w

(L	i	3
		(T	5
D			Cl

f > (Y^xl⁺*$l^tV*^l*V*ł^*t^ł*i)

■ (yV‘fo^ł*l^ł*^l‘V^^ł*J**0

Rys. 2.9. Przykłady minimalizacji funkcji logicznych do postaci NPI. W przykładzie d) podano też postać minimalną wynikającą z innego wyboru grup

zer

W przypadku funkcji niepełnie określonych, w kratki tablicy Karnaugha odpowiadające składnikom nieokreślonym wpisuje się znak x. Tl procesie ml-

o

¹ \ II 11    11 II

0

1*1

■0

*rf

n ii n »

*i^xł

W M H M

N		p	x'	X	00		T|
W	X	$	T		11		0
«	X	sL	3		H	X	0	X	X
»				X	10	X	,xj	X	X

f-*j**A

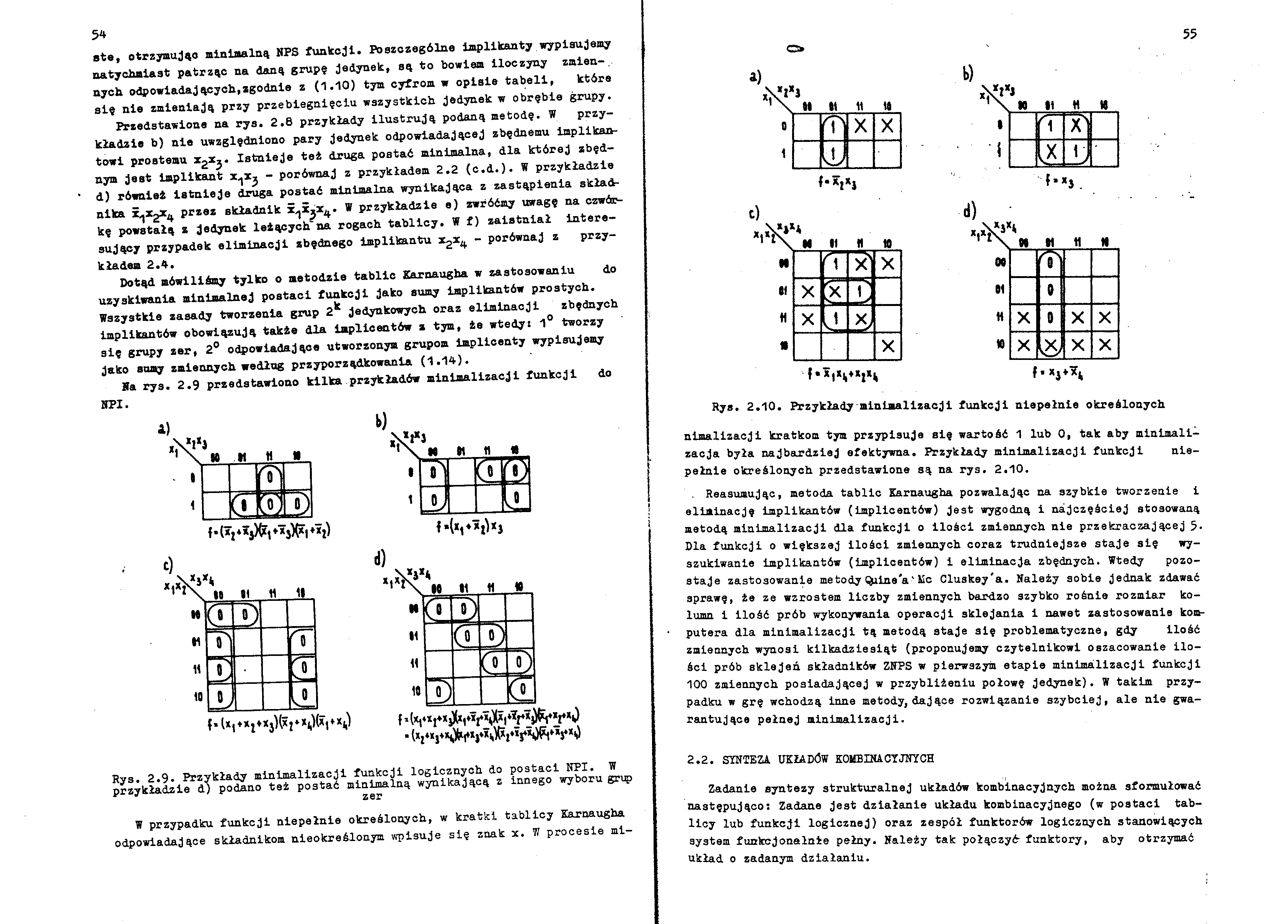
Rys. 2.10. Przykłady minlmallzacji funkcji niepełnie określonych

nimalizacji kratkom tym przypisuje się wartość 1 lub 0, tak aby minimalizacja była najbardziej efektywna. Przykłady minimalizacji funkcji niepełnie określonych przedstawione są na rys. 2.10.

Reasumując, metoda tablic Karnaugha pozwalając na szybkie tworzenie i eliminację implikantów (implicentów) jest wygodną i najczęściej stosowaną metodą minimalizacji dla funkcji o ilości zmiennych nie przekraczającej 5. Dla funkcji o większej ilości zmiennych coraz trudniejsze staje się wyszukiwanie implikantów (implicentów) i eliminacja zbędnych. Wtedy pozostaje zastosowanie metody Ąiine'a'Kc Cluskey'a. Należy sobie jednak zdawać sprawę, że ze wzrostem liczby zmiennych bardzo szybko rośnie rozmiar kolumn i ilość prób wykonywania operacji sklejania i nawet zastosowanie komputera dla minimalizacji tą metodą staje się problematyczne, gdy ilość zmiennych wynosi kilkadziesiąt (proponujemy czytelnikowi oszacowanie ilości prób sklejeń składników ZNPS w pierwszym etapie minimalizacji funkcji 100 zmiennych posiadającej w przybliżeniu połowę jedynek). W takim przypadku w grę wchodzą inne metody, dające rozwiązanie szybciej, ale nie gwarantujące pełnej minimalizacji.

2.2. SYNTEZA UKłADÓW KOMBINACYJNYCH

Zadanie syntezy strukturalnej układów kombinacyjnych można sformułować następująco: Zadane je3t działanie układu kombinacyjnego (w postaci tablicy lub funkcji logicznej) oraz zespół funktorów logicznych stanowiących system funkcjonalnie pełny. Należy tak połączyć- funktory, aby otrzymać układ o zadanym działaniu.