054 055

sta, otrzymując minimalną HPS funkcji. Fnazczególna Impliknnty wypisujemy natychmiast patrząc na daną grupę Jedynek, aą to bowiem Iloczyny zmian-, nych odpowiadających,zgodnie z (1.10) tym cyfrom w opisie tabeli, kt6re się nie zmieniają przy przebiegnięciu wszystkich Jedynek w obrębie grupy.

Przedstawione na rys. 2.8 przykłady ilustrują podaną metodę. W przykładzie b) nie uwzględniono pary Jedynek odpowiadającej zbędnemu lmplikan-towi prostemu ^₂^xy Istnieje też druga postać minimalna, dla której zbędnym Jest lmpllkant    - porównaj z przykładem 2.2 (c.d.). W przykładzie

d) również istnieje druga postać minimalna wynikająca z zastąpienia składnika x^x₂x_ił przez składnik x^x^x^. W przykładzie e) zwróćmy uwagę na czwórkę powstałą z Jedynek leżących'na rogach tablicy. V f) zaistniał interesujący przypadek eliminacji zbędnego implikantu *₂^XĄ ~ P^or*^wnaJ z przykładem 2.4.

Dotąd mówiliśmy tylko o metodzie tablic Kar naugha w zastosowaniu do uzyskiwania minimalnej postaci funkcji jako sumy impllkantów prostych. Wszystkie zasady tworzenia grup 2* jedynkowych oraz eliminacji zbędnych impllkantów obowiązują także dla implieentów z tym, żs wtedyt 1° tworzy się grupy zer, 2° odpowiadające utworzonym grupom implicenty wypisujemy Jako sumy zmiennych według przyporządkowania (1.14).

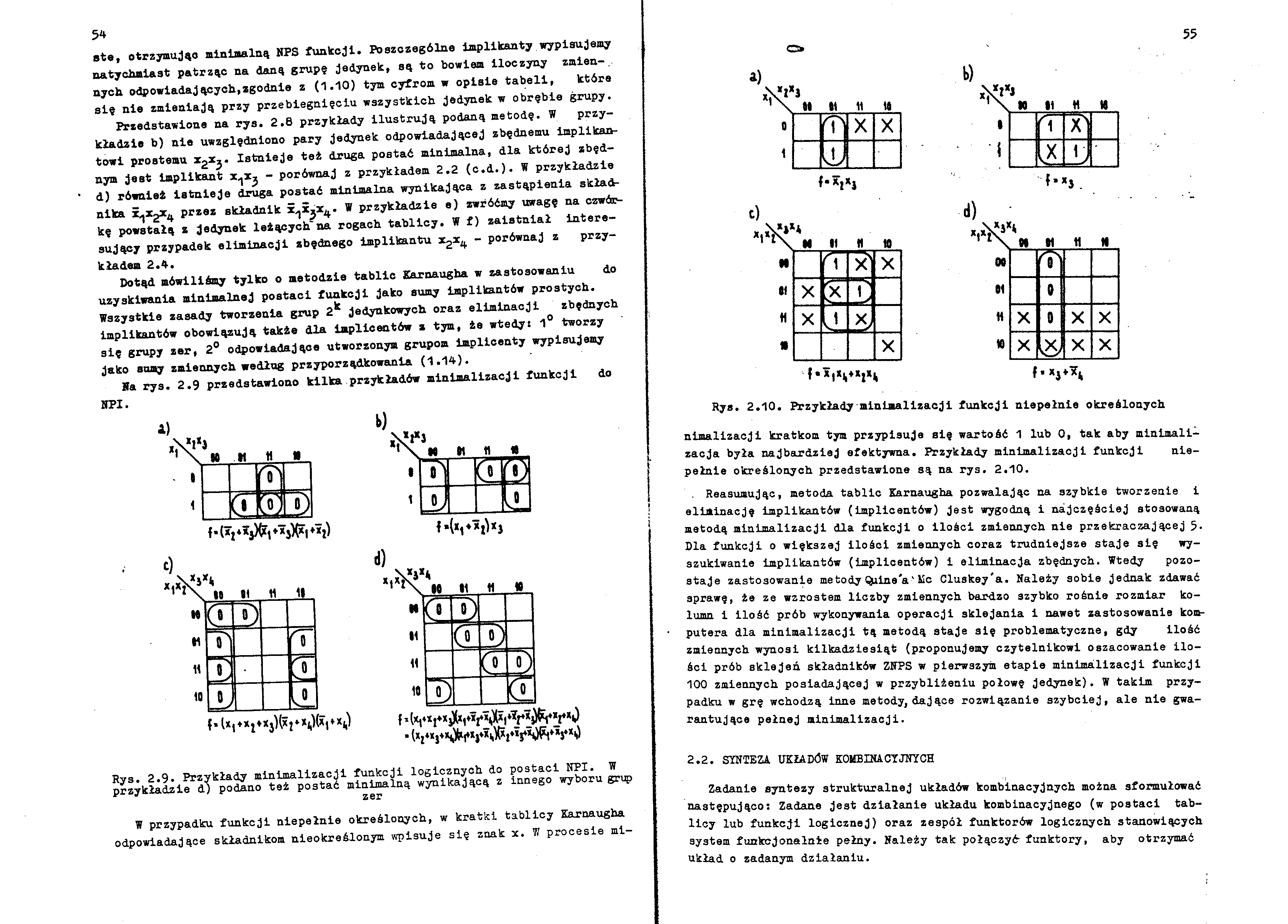
Ha rys. 2.9 przedstawiono kilka przykładów minimalizacji funkcji do BPI.

A)

b)

MMMM

	Jfi
	GE!	$

MMMM

hfph

<0

MMMM

G	J)	ZL		N	F
T			T	M		(■	0
X			G	ii			G	$
31			Ll	10	D

Hx, ł*j ♦Xj)(x_I»x*Mx, ♦ *_k)

f * (v^xI^łX^l^łYS'P|^łV*J^t^ł*I‘*i)

• (*2«j^łX0M|^ł*sXyV^xfo^łV^x0

Rys. 2.9. Przykłady minimalizacji funkcji logicznych do postaci NPI. W przykładzie d) podano też postać minimalną wynikającą z innego wyboru grup

zer

W przypadku funkcji niepełnie określonych, w kratki tablicy Karnaugba odpowiadające składnikom nieokreślonym wpisuje się znak x. W procesie ml-

o

i)	'3 M	11	11	11
0				X
1
			*3
c)		11	II	n
N		ń	x'	X
H	X		T
11	X	U	X,
»				X

b)

d)

*rt

*3^xł

o«

01

«

w

00 M

	^f*i
	0
X	0	X	X
X	y	X	X

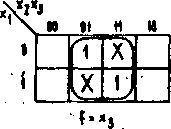
Rys. 2.10. Przykłady minimalizacji funkcji niepełnie określonych

nimalizacji kratkom tym przypisuje się wartość 1 lub O, tak aby minimalizacja była najbardziej efektywna. Przykłady minimalizacji funkcji niepełnie określonych przedstawione są na rys. 2.10.

. Reasumując, metoda tablic Karnaugha pozwalając na szybkie tworzenie i eliminacją impllkantów (implicentów) Jest wygodną i najczęściej stosowaną metodą minimalizacji dla funkcji o ilości zmiennych nie przekraczającej 5-Dla funkcji o większej ilości zmiennych coraz trudniejsze staje się wyszukiwanie impllkantów (implicentów) i eliminacja zbędnych. Wtedy pozostaje zastosowanie metody t>ilne'a‘Kc Cluskey'a. Kalety sobie Jednak zdawać sprawę, że ze wzrostem liczby zmiennych bardzo szybko rośnie rozmiar kolumn i ilość prób wykonywania operacji sklejania i nawet zastosowanie komputera dla minimalizacji tą metodą staje się problematyczne, gdy ilość zmiennych wynosi kilkadziesiąt (proponujemy czytelnikowi oszacowanie ilości prób sklejeń składników ZNPS w pierwszym etapie minimalizacji funkcji 100 zmiennych posiadającej w przybliżeniu połowę jedynek). W takim przypadku w grę wchodzą inne metody, dające rozwiązanie szybciej, ale nie gwarantujące pełnej minimalizacji.

2.2. SYNTEZA UKZADÓW KOMBINACYJNYCH

Zadanie syntezy strukturalnej układów kombinacyjnych można sformułować następująco: Zadane Je3t działanie układu kombinacyjnego (w postaci tablicy lub funkcji logicznej) oraz zespół funktorów logicznych stanowiących system funkcjonalnie pełny. Należy tak połączyć- funktory, aby otrzymać układ o zadanym działaniu.