104 105

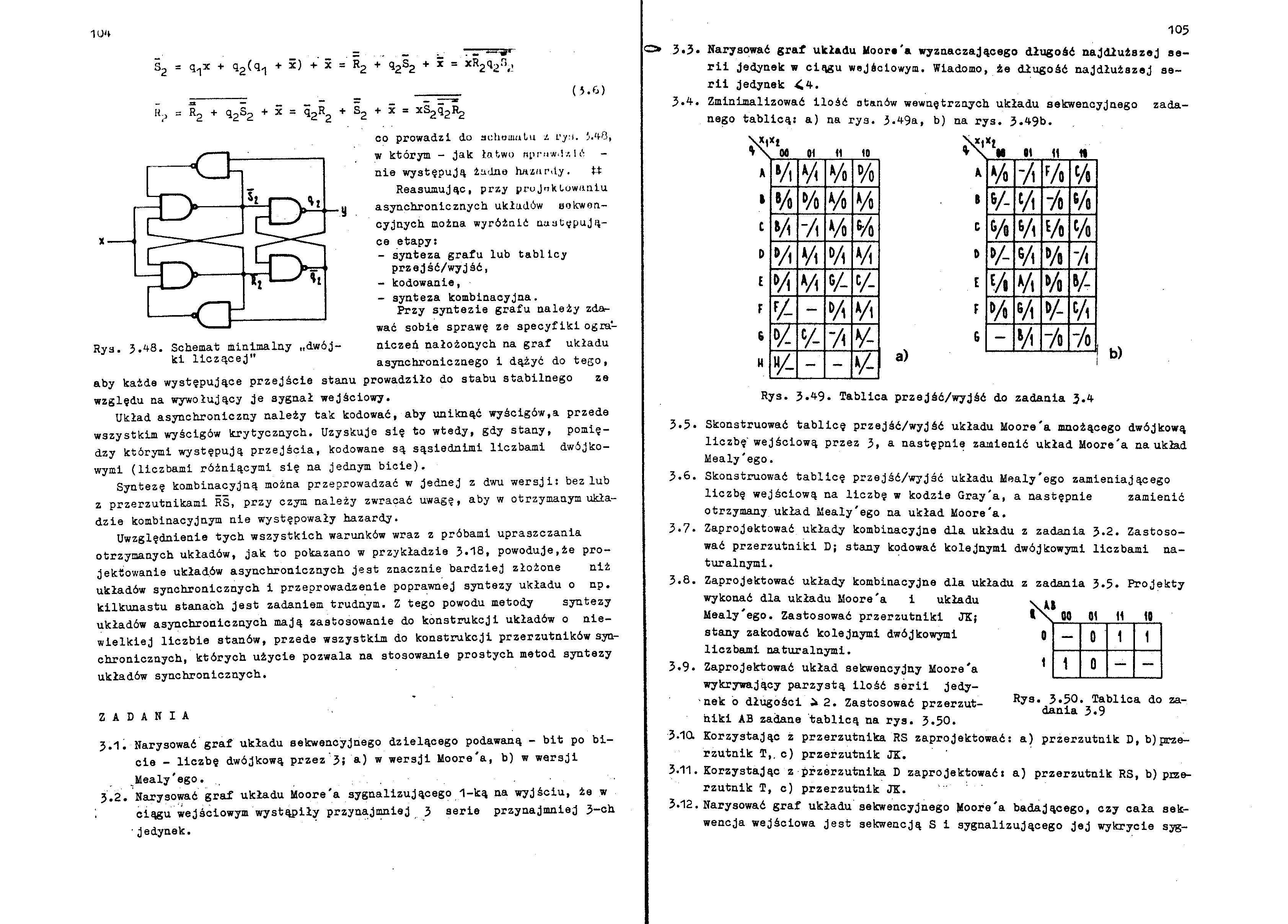
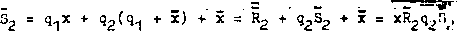
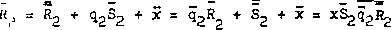
(5.6)

X

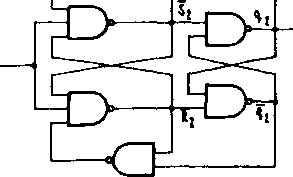
Rys. 3.48. Schemat minimalny „dwójki liczącej"

co prowadzi do schematu z t'y:i. Vł-0, w którym - Jak łatwo npmwdzI ć -nie występują ludne hazardy. it

Reasumując, przy projektowaniu asynchronicznych układów sokwen-cyjnych można wyróżnić następujące etapy:

- synteza grafu lub tablicy

przejść/wyjść,

-    kodowanie,

-    synteza kombinacyjna.

Przy syntezie grafu należy zdawać sobie sprawę ze specyfiki ograt niczeń nałożonych na graf układu asynchronicznego i dążyć do tego,

aby każde występujące przejście stanu prowadziło do stabu stabilnego ze względu na wywołujący je sygnał wejściowy.

Układ asynchroniczny należy tak kodować, aby uniknąć wyścigów,a przede wszystkim wyścigów krytycznych. Uzyskuje się to wtedy, gdy stany, pomiędzy którymi występują przejścia, kodowane są sąsiednimi liczbami dwójkowymi (liczbami różniącymi się na jednym bicie).

Syntezę kombinacyjną można przeprowadzać w jednej z dwu wersji: bez lub z przerzutnikami RS, przy czym należy zwracać uwagę, aby w otrzymanym układzie kombinacyjnym nie występowały hazardy.

Uwzględnienie tych wszystkich warunków wraz z próbami upraszczania otrzymanych układów, jak to pokazano w przykładzie 3.18, powoduje,że projektowanie układów asynchronicznych jest znacznie bardziej złożone niż układów synchronicznych i przeprowadzenie poprawnej syntezy układu o np. kilkunastu stanach jest zadaniem trudnym. Z tego powodu metody syntezy układów asynchronicznych mają zastosowanie do konstrukcji układów o niewielkiej liczbie stanów, przede wszystkim do konstrukcji przerzutników synchronicznych, których użycie pozwala na stosowanie prostych metod syntezy układów synchronicznych.

ZADANIA

3.1.    Narysować graf układu sekwencyjnego dzielącego podawaną - bit po bicie - liczbę dwójkową przez 3i a) w wersji Moore'a, b) w wersji iiealy'ego.

3.2.    Narysować graf układu Moore'a sygnalizującego 1-ką na wyjściu, że w

l    ciągu wejściowym wystąpiły przynajmniej 3 serie przynajmniej 3-ch

• jedynek.

o

3.3

3-4

Narysować graf układu Uoora'a wyznaczającego długość najdłuższej serii jedynek w ciągu wejściowym. Wiadomo, że długość najdłuższej serii jedynek <4.

Zminimalizować ilość stanów wewnętrznych układu sekwencyjnego zadanego tablicą: a) na rys. 3-49a, b) na rys. 3.49b.

Wt

Qt 11

00    01    <1 to

'A	V.	Vó	%
^B/o	»/o	Vo	yó
*/1	-A	Vo	Vó
^D/1	*/i	°/1	Vi
°/	Vi	«/-	^c/-
^F/-	-	»A	V\
	V-	-A	V-
»/-	-	-	V-

a)

tyÓ	-A	^F/o	^c/«
V-	^£/i	"/o	tyfl
6/fl	^6/i	V«	t/o
>/-	^s/i		-A
^E/l	Vt	^6/fl	*/-
»/a	^6/t	>/-	ya
-	'A	"/o	~/o

b)

Rys. 3.49. Tablica przejść/wyjść do zadania J.4

3.5* Skonstruować tablicę przejść/wyjść układu Moore'a mnożącego dwójkową liczbę wejściową przez 3. a następnie zamienić układ Moore'a na układ Mealy'ego.

3.6. Skonstruować tablicę przejść/wyjść układu Mealy'ego zamieniającego

liczbę wejściową na liczbę w kodzie Gray'a, a następnie zamienić otrzymany układ Mealy'ego na układ Moore'a.

3*7. Zaprojektować układy kombinacyjne dla układu z zadania 3-2. Zastosować przerzutniki D; stany kodować kolejnymi dwójkowymi liczbami naturalnymi.

l\ 00		01	u	10
0	—	0	1	1
i	1	0	—	—

3.8.    Zaprojektować układy kombinacyjne dla układu z zadania 3*5. Projekty wykonać dla układu Moore'a i układu Mealy'ego. Zastosować przerzutniki JKj stany zakodować kolejnymi dwójkowymi liczbami naturalnymi.

Rys. 3.30. Tablica do zadania 3.9

a) przerzutnik D, b) prze-

3.9.    Zaprojektować układ sekwencyjny Moore'a wykrywający parzystą ilość serii jedynek o długości i 2. Zastosować przerzut-hiki AB zadane tablicą na rys. 3.50.

3-10. Korzystając ż przerzutnika RS zaprojektować: rzutnik T,. c) przerzutnik JK.

3.11.    Korzystając z przerzutnika D zaprojektować: a) przerzutnik RS, b) przerzutnik T, c) przerzutnik JK.

3.12. Narysować graf układu sekwencyjnego Moore'a badającego, czy cała sekwencja wejściowa jest sekwencją S i sygnalizującego Jej wykrycie syg-