212 213

212

t l 4 I K U (MU » »t

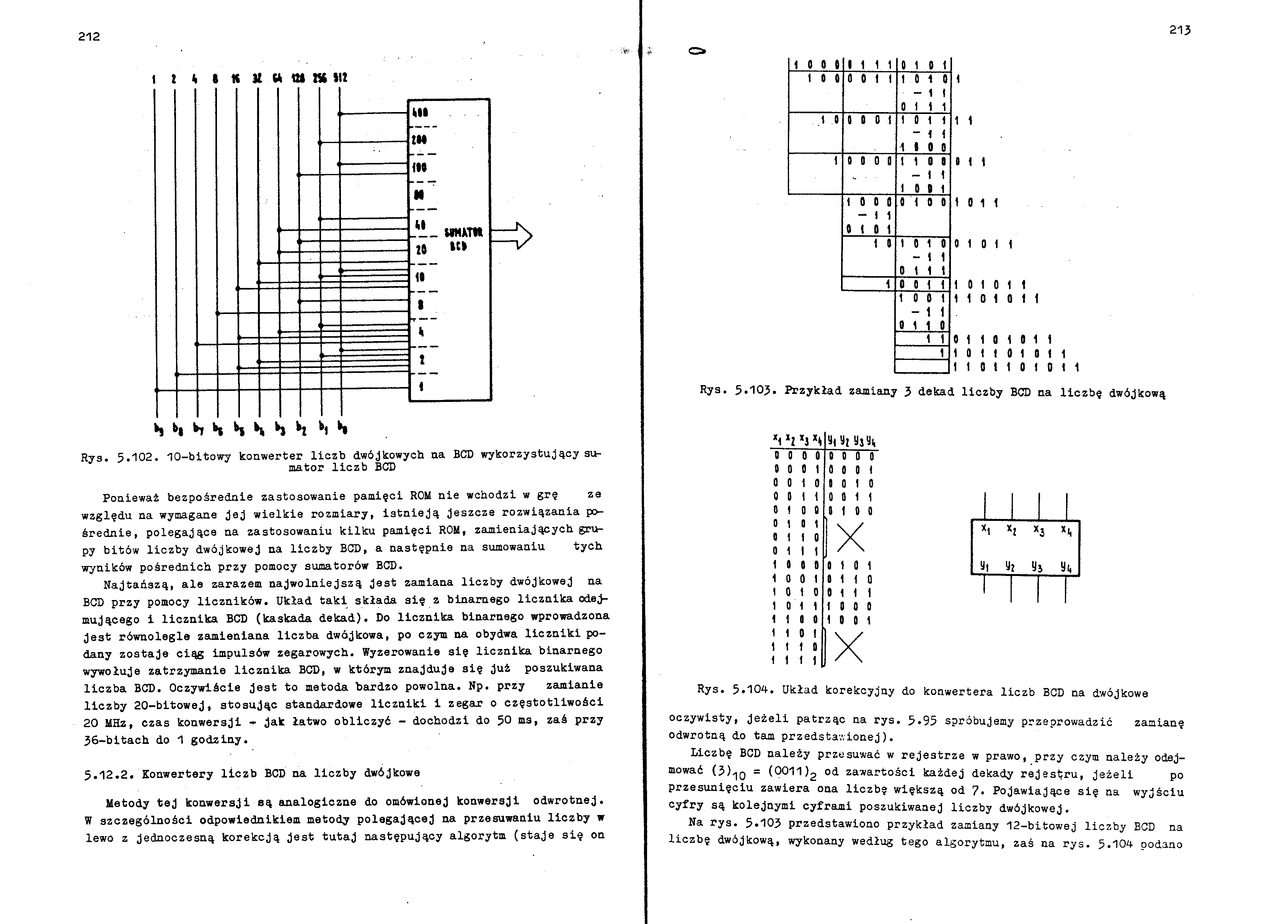
Rys. 5.102. 10-bitowy konwerter liczb dwójkowych na BCD wykorzystujący sumator liczb BCD

Ponieważ bezpośrednie zastosowanie pamięci ROM nie wchodzi w grę ze względu na wymagane jej wielkie rozmiary, istnieją jeszcze rozwiązania pośrednie, polegające na zastosowaniu kilku pamięci ROM, zamieniających grupy bitów liczby dwójkowej na liczby BCD, a następnie na sumowaniu tych wyników pośrednich przy pomocy sumatorów BCD.

Najtańszą, ale zarazem najwolniejszą jest zamiana liczby dwójkowej na BCD przy pomocy liczników. Układ taki składa się z binarnego licznika odejmującego i licznika BCD (kaskada dekad). Do licznika binarnego wprowadzona jest równolegle zamieniana liczba dwójkowa, po czym na obydwa liczniki podany zostaje ciąg impulsów zegarowych. Wyzerowanie się licznika binarnego wywołuje zatrzymanie licznika BCD, w którym znajduje się już poszukiwana liczba BCD. Oczywiście jest to metoda bardzo powolna. Np. przy zamianie liczby 20-bitowej, stosując standardowe liczniki i zegar o częstotliwości 20 MHz, czas konwersji - Jak łatwo obliczyć - dochodzi do 50 ms, zaś przy 36-bitach do 1 godziny.

5.12.2. Konwertery liczb BCD na liczby dwójkowe

Metody tej konwersji są analogiczne do omówionej konwersji odwrotnej.

W szczególności odpowiednikiem metody polegającej na przesuwaniu liczby w lewo z jednoczesną korekcją jest tutaj następujący algorytm (staje się on

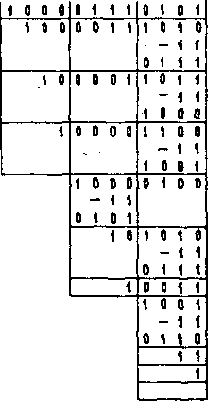
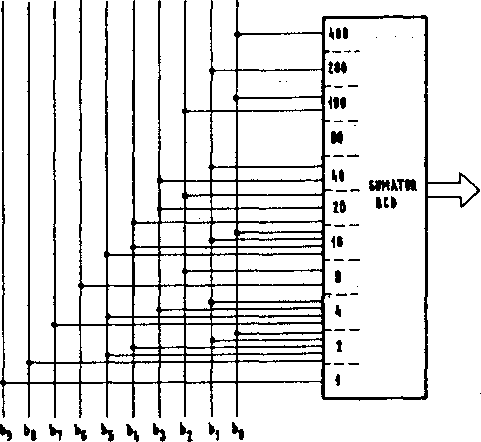
Rys. 5.103. Przykład zamiany 3 dekad liczby BCD na liczbę dwójkową

*1 *1 *1 ^xł	si h yjso
0 0 0 0	0000
0 0 0 t	0 0 0 1
0 0)0	0 0(0
4 0 ) t	0 0 11 I I I I
0(00	0100 1 1 1 1
0 10)	V	*1 *! ^x3 *1,
0 110	X
0 111	1 ^/x
10 0 0	0 10 1	ut y* yj yt,
1001	0 110
10 10	0 111 III
10 11	10 0 0
110 0	10 0 1
110 1
1110 lit)	IX

Rys. 5.1CW. Układ korekcyjny do konwertera liczb BCD na dwójkowe

oczywisty, jeżeli patrząc na rys. 5*95 spróbujemy przeprowadzić zamianę odwrotną do tam przedstawionej).

Liczbę BCD należy przesuwać w rejestrze w prawo, przy czym należy odejmować (3)-]0 = (0011 )₂ od zawartości każdej dekady rejestru, jeżeli po przesunięciu zawiera ona liczbę większą od ?. Pojawiające się na wyjściu cyfry są kolejnymi cyframi poszukiwanej liczby dwójkowej.

Na rys. 5*103 przedstawiono przykład zamiany 12-bitowej liczby BCD na liczbę dwójkową, wykonany według tego algorytmu, zaś na rys. 5.104 podano