3

Nm

KOLOKWIUM NAI (15.05.2002)

Zadanie 1:

Skonstruuj jak najprostsząjednokierunkową sieć perceptronów o trzech wejściach i jednym wyjściu, zgodną z poniższymi danymi:

Wejście 1	Wejście2 Wejście3	Wyjście
0	“o ĆT i	i i i
0	1 ;	1
1	0 j 1	^1 ; i
1	Ł i o	0 t

Zadanie 2:

Zaproponuj algorytm zachłanny szukający dla danegu grafu nieskierowanego maksymalnego zbioru krawędzi niezależnych, tzn. takiego zbioru krawędzi, z któr/cn każda para nie ma wspólnych wierzchołków. Oszacuj złożoność czasową tego

• . j.~*    '    ' tf r '    _ti    • i "

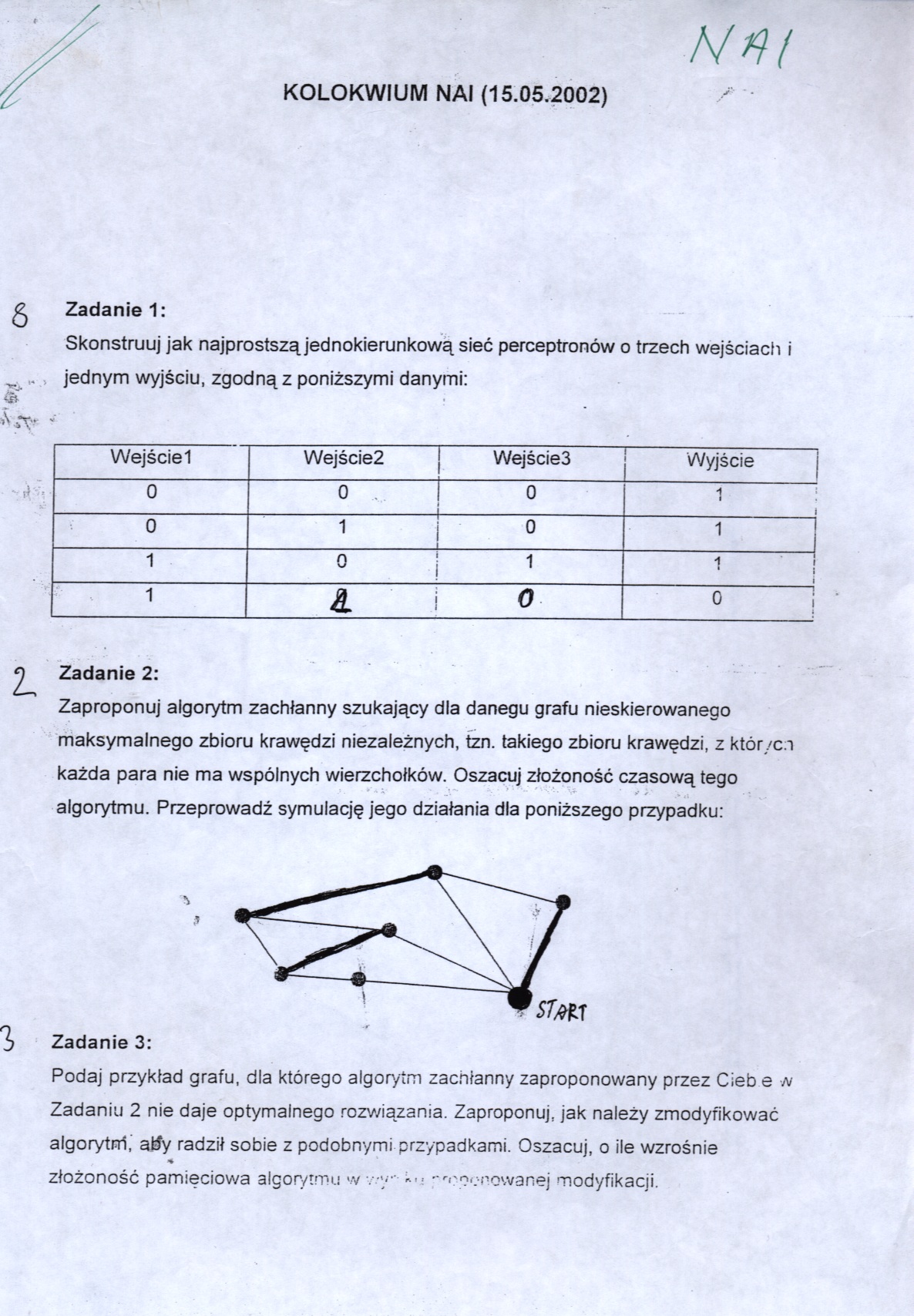
algorytmu. Przeprowadź symulację jego działania dla poniższego przypadku:

Zadanie 3:

Podaj przykład grafu, dla którego algon/tm zac.ołanny zaproponowany przez Cieb e w Zadaniu 2 nie daje optymalnego rozwiązania. Zaproponuj, jak należy zmodyfikować algorytrri,' afcfy radził sobie z podobnymi przypadkami. Oszacuj, o ile wzrośnie złożoność pamięciowa algorytmu wwy -'■oporowanej modyfikacji.