4504

I soapolonych (^J -g >-

Itczby z«'spolonej (1.5).

^‘erwinatkowj

•nio UcsL

Pr^ylctedy

P«yfc#ae# 3.1

Stosu »r*c posta<5 wykładniczy liczby zespolonej

^{z roaw}i^*«^ podane równania:

W

*>>

Zastępując symbolem e ’ " »vyrazenie cw^ + isin wwUęPW

.i x k r-(cos v==» -f- sin yg) otrzym|

_    __ i bólem e'^v wyrażenie

nej łiczby aeapoJonęj

_t    r = re'*'. Pray rozwiązywaniu równan —-w----* *«S». ze <Jwie nic-

‘erowc U<tm t>y zespolone są sobie równe wtedy « tylko wtedy, gdy ich moduły są równe. ich argumenty różnią si« o wielokrotnoó    ^lzn* ^d,a M* ““ ^{rj e} *• ^ “ ^rao **• r,, _r, > _0<

*^BI "^1B1^    ^    _ _^_a -f —fj = ra oraz ^1 =    -+- 21*jt, Ar € Z.

l^icsba z = O spełnia równanie    — ⁴    - ^Nicc,i    ^    «d*ie _r

O ^ ^ < 2^. Wówczas 3- «= r-er — ** oraz, ze wzoru do Moivre’a, (W)    ==

r², a więc

___ / *----* ••^a««Mnieiryci.

—^Ł,n-^{V P}°*^tać wyk|_a«laiiic*4 tej liczby l.edzicmy korzystać z tego. że dwie „i/

i - 1-trt r-W V O < I « — :»Ł.    -___■ - ■

Dal

ej

W = ⁴ /-*/

*e’°

/ r-* =⁴*

l -6^ =

{

O -f- 2Arrr, 1* € Z a/2

_r = O lub r

V, ==    / = o, a, 2, 3. 4, s.

Rozwiązaniami równania są zatem licac by

= O.

V2.

sj

s". S4

Są one przedstawione na rysunku ponizej

Z in —

S3

r«

-*3.

—««

b) Równoważnie możemy napisać, że |a|¹ • ₄ ■ l_|\.    ,» . .    ..

gdzie r > 0. 0 ^ ¹» < 2¹ Wówcaaa    ^r    1

■•i#

)

keZ

e"* i* r⁸.r»

•fi ■ « - 3* + 2k».

f ^r € (O.oo),

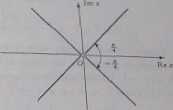
Rozwiązania równania tworzą więc dwie proste nachylone do osi rzeczywistej pod kątami — oraz — — i przechodzące prze¹ punkt O, ale bez tego punktu (rysunek).

• Przykład 3.2

Stosując wzory Eulera przedstawić cos^{6 1} w postaci sumy sinusów i coeinusów wielokrotności kąta x.

Rozwiązanie

e^ix + e”'¹

Mamy cos z -5-—• Stosując teraz wzór dwumianowy Newtona otrzymamy

«• ¹ = Ja 1

⁼ 2¹

[(0) (¹“)¹    +II (-“i¹ («-“)■+|§ («“/ («-)'

⁺(a)    (•‘“i¹+(;) (•■■)' (.-)•+(;) («“)° («-)¹]

= i (c^1ix + 5e³² + lOe'® + lOe"'¹ + 5e'³ⁱ¹ + e“^si1)

V⁵¹ + ę~^lłz _{+ 5}c'^3l+e-^,aj _{+ l0}ę^4_ęŻ

-i

= — (cos5i + 5cos 3¹ + lOcosi).

1

Przykład 3.3

2

Korzystając z definicji obliczyć podane pierwiastki: a) 3; b) ^S.