7 6

Piotr Bieranowski - ćwiczenia z WYTRZYMAŁOŚCI MATERIAŁÓW, CZ. VII.

(p = 180°-2ó? = 60 [°]

Naprężenie normalne i naprężenie styczne wynoszą odpowiednio

(7_a = OC- AC = OC- rcos (p = 30 -20cos 60° = +20 [MPa], z_a = +AN = +r sin (p = +20sin 60° = +17 [MPa].

HIPOTEZY WYTRZYMAŁOŚCIOWE. WYTRZYMAŁOŚĆ ZŁOŻONA SŁOWO WSTĘPNE

W odniesieniu do materiałów izotropowych mających granicę plastyczności (wyraźną lub umowną) najlepszą zgodność z doświadczeniem daje hipoteza wytrzymałościowa Hubera [1].

Jeżeli stan napięcia w najbardziej obciążonym punkcie ciała jest wyrażony przez naprężenie główne: cr_x>(7₂> a₃, wówczas naprężenia zredukowane są określone wzorem

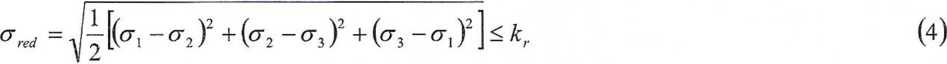
Gdy stan naprężeń jest określony przez naprężenie normalne cr i styczne z , wówczas

cr_red = -Ja¹ +3x² < k_r    (5)

W obliczeniach dotyczących materiałów plastycznych obok hipotezy Hubera stosuję się również hipotezę r_max (największych naprężeń stycznych, Coulomba), dającą w zastosowaniach prostsze zależności. Naprężenie zredukowane dla stanu napięcia określonego przez naprężenia główne a₁ > cr, > a₃ wyraża się wzorem

^=cri    (6)

zaś dla stanów określonych naprężeniami normalnymi u i stycznymi z

^ared =+7² +4 r² <k_r    (j)

Dla materiałów kruchych, takich jak żeliwo, odlewy z metali kolorowych, stosuje się hipotezę największego wydłużenia względnego £_max

str. 6