Image1633
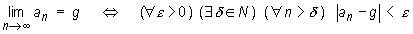
lim an = g ś=> (Vs >0) (33eN) {Vn > 3) |an -g| < £
Wyszukiwarka
Podobne podstrony:
Image1970 lim an = + co .
GRANICA2 lim an = g:<=> V 3 V d(an,g) <£ (-jest to def granicy ciągu w przestrzeń i metrycz
image1667 lim n —>lim 1 a = O => — co n —> co an =
image1668 lim n —>lim 1 a = O => — co n —> co an =
Image1702 lim fĄ 1 1 1 + — II Sb lim fi-±l an t 11J an t 11 /
Image1978 lim -^ = 1 + CO = 0, bo an = n —> + c°
Image1999 lim + (», bo an = n + » bfj = 2-fń —> 2-1 = 2
Lemat 2.2 Niech (Vn 6 A/*) O < afl < fcfl oraz lim bn = 0. Wtedy lim an = 0. n—oo
Image2012 lim an = + co => lim bn=+<^>
więcej podobnych podstron