Image1955
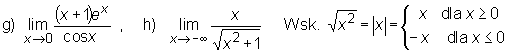
g) lim
x-»0
X+l)e*
cosx
h) lim -== x^"“ Vx2 + 1
Wsk.

J x dla x > O j-x dlax<0
Wyszukiwarka
Podobne podstrony:
Image163 a = lim AŹ-»0 ~V1 te = lim a^ov(Ą + AQ-v(*i) te
image1641 lim a*n —> co g V &> 0YląYl > «0"g <
Image1906 6) lim x-»« lnx = co , lim lnx = -® x-»0+
Image1911 • lim x-»-« = sgn CO x2 -4 (~x?-4 x2 -4 iczniki mianownik są wielomianam
Image1921 x+2 lim x-»( 1 + x +1 = 42 = 16 ponieważ lim x-»0l 1 + X + 1 = 4 oraz lim (x+2) = 2 x-»0
Image1922 lim 1 X-»TOx +3 lim X-»" -2x"= lim X—> “ -2x + 3, x+3 “2 x+3 x + 3 o X- =
Image1932 1 1 lim xsin— = O gdyż lim x = O i funkcja sin— jest ograniczona, bo x-»0
Image1906 6) lim x-»« lnx = co , lim lnx = -® x-»0+
Image1922 lim 1 X-»TO x +3 lim X-»" -2x" = lim X—> “ -2 x + 3, x+3 “2 x+3 o x“ x
Image131 — = lim ds AJ-»04r ńs
Image1633 lim an = g ś=> (Vs >0) (33eN) {Vn > 3)
więcej podobnych podstron