Image2224
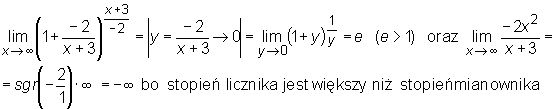
lim 1 + —-x-»«l x + 3
x+3
-2
-2 X + 3
■» O = lim (1 + y)y =e y^O
(e>1)
oraz
lim
x-»«
-2x2 x + 3
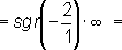
— co
bo stopień licznika jest większy niż stopieńmianownika
Wyszukiwarka
Podobne podstrony:
Image2228 lim sgnx= lim 1=1 oraz lim sgnx= lim (-1) = —1.zaś sgn 0 = 0. x-»0+
Image2002 * lim ■ ń„) = [± 0= -o] = ?
Image2012 lim an = + co => lim bn=+<^>
Image2014 1. lim np = + co (p>0) 2. lim np=0 (p < 0)
Image2016 5. lim %fń= 1 n-¥<» r>
Image2018 3 3 lim — = 0 (a dowolne) 10. lim — = + co (a > 1, p > 0) n I
Image2022 • lim 3 r? +1 n + 2 3 ns +1 3n2 +1 n _ + co = lim n = lim + co + 0 + co n +
Image2033 lim lim (j2n + 5 - 42 n + 3) = [+ co - (+ co)]■/2n + 5 - 42 n + 3j,j2n + 5 + 42 n + 3 j 42
Image2109 lim cS„ {+ « gdy c > O - oo, gdy c < O
Image2154 3 lim ^5“ = 2- lim $l5/ lim %fń = 2 > 1,
Image2210 lim f(x) = g lub f(x) x^x0 x^x0 >9-
Image2213 *9 lim f(x) =g lub f(x)--- x-»x0+ x^xo
Image2219 lim X-¥ 2x-2 17x + 3 - 2-Jx ztwierdzenianie można skorzystać- funkcjanie jest określona w
Image2309 lim f(x) = -co lub lim f(x) = <*> x-*a~ x^>a~
Image2336 X lim - x^olnx = 0. lim X X = —co x-»r lim -x^i+ lnx X = co lim — xh>®
Image2952x • lim n2 +2-n + co -lim ( I- — r i- — + 2 - n In1 + 2 + n L __J L_ J r r?—
028(1) Wyznaczyć granice: 86. lim (
więcej podobnych podstron