Image227
DC
^BA
00
01
11
10
10
11
01
00
JO 01 1 1 10
X=1
X=Q-
|
0 |
1 |
3 |
2 |
|
A |
5 |
7 |
6 |
|
12 |
13 |
15 |
14 |
|
8 |
9 |
11 |
10 |
|
8 |
7 |
5 |
6 |
|
A |
3 |
1 |
2 |
|
12 |
11 |
9 |
10 |
|
0 |
15 |
13 |
14 |
X=1
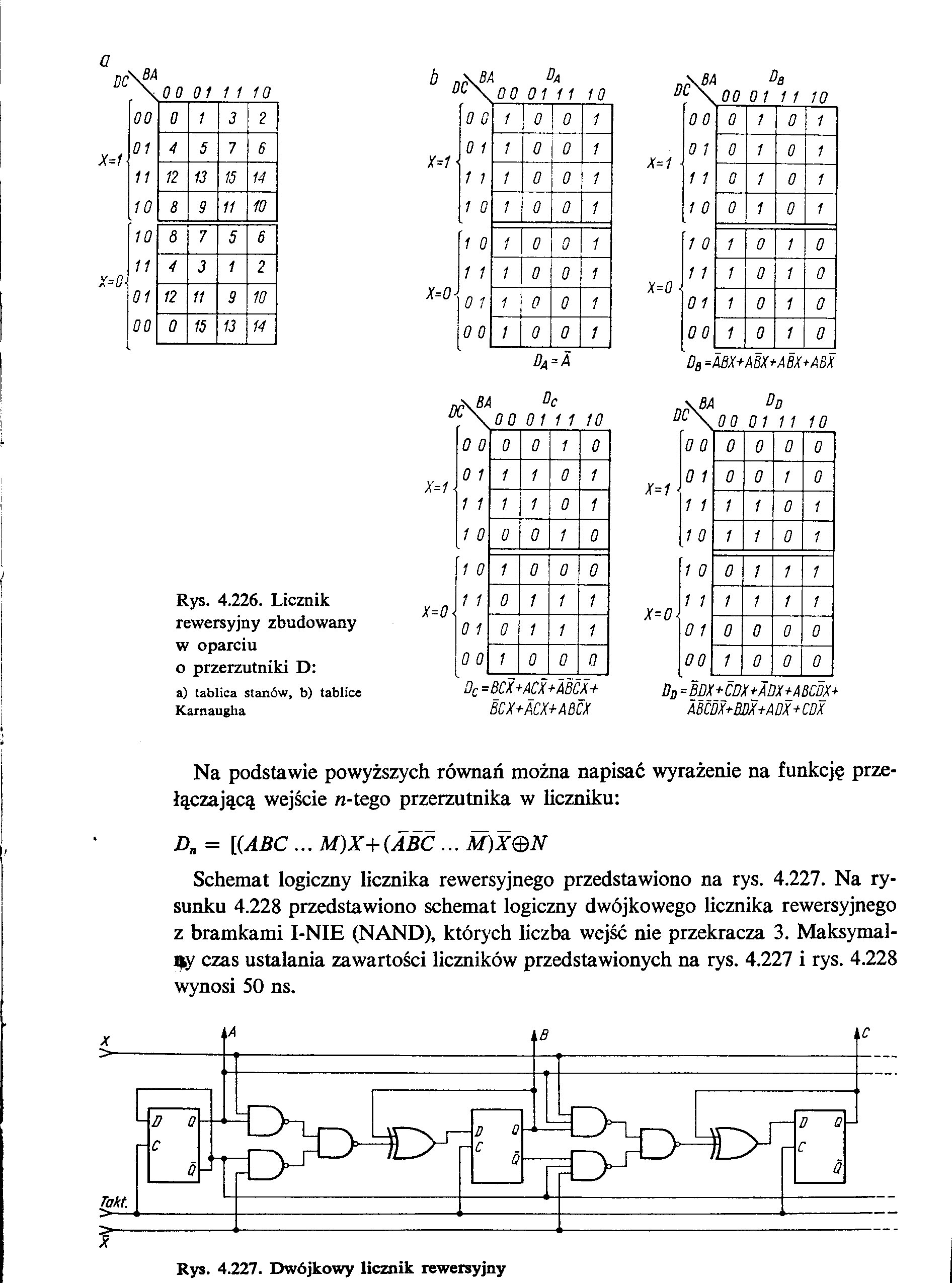
Rys. 4.226. Licznik rewersyjny zbudowany w oparciu o przerzutniki D:
a) tablica stanów, b) tablice Karnaugha
X=0
b DCs
X=f
DCs
|
A 00 |
Da 0111 |
10 |
mJoo |
Da 0111 |
w | ||||
|
J / |
0 |
! o |
1 |
0 0 |
0 |
1 |
0 |
1 | |
|
1 |
0 |
0 |
1 |
X=1 |
0 1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
11 |
0 |
1 |
0 |
1 | |
|
' 1 |
0 |
0 |
1 |
1 0 |
0 |
1 |
0 |
1 | |
|
4 5 |
0 |
0 |
1 |
' 1 0 |
1 |
0 |
1 |
0 | |
|
1 |
0 |
0 |
1 |
X=0 < |
11 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
01 |
1 |
0 |
1 |
0 | |
|
1 |
0 |
0 |
1 |
0 0 |
1 |
0 |
1 |
0 | |
|
Da |
= A |
Db=ABX+ABX+ABX+ABX | |||||||
|
4 00 |
D 01 |
c 1 1 |
10 |
00 |
Dd 0111 |
10 | |||
|
0 |
0 |
1 |
0 |
0 0 |
0 |
0 |
0 |
0 | |
|
1 |
1 |
0 |
1 |
x=u |
0 1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 1 |
1 |
1 |
0 |
1 | |
|
0 |
0 |
1 |
0 |
1 0 |
1 |
1 |
0 |
1 | |
|
1 |
0 |
0 |
0 |
1 0 |
0 |
1 |
1 |
1 | |
|
0 |
1 |
1 |
1 |
x=o< |
1 1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 1 |
0 |
0 |
0 |
0 | |
|
1 |
0 |
0 |
0 |
00 |
1 |
0 |
0 |
0 | |
Dc=8CX+ACX+ABCX+
BCX+ACX+ABCX
Dd=BDX+CDX+ADX+JBCBX+
Mbx+wx+abx+cbx
Na podstawie powyższych równań można napisać wyrażenie na funkcję przełączającą wejście n-tego przerzutnika w liczniku:
Dn = [(ABC ... M)X+(ABC... M)X@N
Schemat logiczny licznika rewersyjnego przedstawiono na rys. 4.227. Na rysunku 4.228 przedstawiono schemat logiczny dwójkowego licznika rewersyjnego z bramkami I-NIE (NAND), których liczba wejść nie przekracza 3. Maksymalny czas ustalania zawartości liczników przedstawionych na rys. 4.227 i rys. 4.228 wynosi 50 ns.
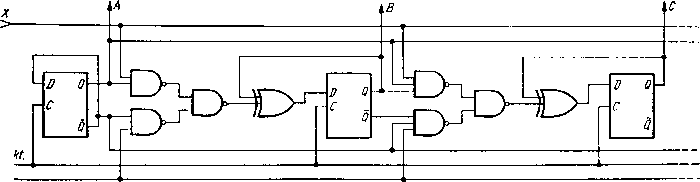
Rys. 4.227. Dwójkowy licznik rewersyjny
Wyszukiwarka
Podobne podstrony:
Image246 Rd = £sin 60° = 12*0,86 * 10,3tf Rs = 0cos6Oł =12*0,5 = 6bl.
gwiazdki 4b SNOWFLAKE D SNOWFLAKE C in any ch-10 loop. (4 dc. ch 5. 4 dc. ch 1) In each ch-10 loop a
sA. YŁ- /W<* HEADOUARTER DC /G/2C: . IB ARMY GROUP. 10 t
rosebud ornaments 7 skip next ch-3 sp, (dc in next st, ch 1) 10 times. dc in noxt st, ch 3. skip&n
image26 (17) 25 krów. 15 krów. 10 krów. 15 krów. 17 krów. 5 krów. 50 krów.
test OC X ?E 001368 ł 9BG-‘<L092 La 1 ,2lM.2 OP KOG DC X oc 00 5 390
DSC00049 (10) !■ 3. Orientacja wewnętrzna *cłjęe Jo^vł2u. wwuMJO Elementami orientacji wewnętrznej g
uiim v* ^ i Kn ■ V1*T R* ba • t iv 3 /I ylVI /. * 11 ,ł1 ■ ■ f j
slide0338 image273 0CATIA V5 - [śruby_01.CATPart] □ Start TeamPDM File Edit View Insert lools Window
10 (140) [y„3 jO,t>-3 4 Tg?« - g,~~53 - l^r pc^-Vo^<ovt,<Ł pOcf? 4- 0 yf
10(6) J----4---1... ■V; ł*J. * ctcJc o uiaitc JO ku tJłioJd iii q eiętkto<J fhtćyout a^ct ^ -Slfa
więcej podobnych podstron