Image2906
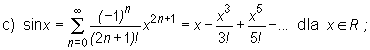
c) sinx = X
(-1/
x
x
= x~ — + — dla xeR ;
n=0 (2n + ])!
3/ 5/
Wyszukiwarka
Podobne podstrony:
Image2907 ci) cosx = y —dla xeR n=Ó (2n)t At 6/
Image2852 gdzie Rn(x) = fn(c) ni (x ~X{])n dla pewnego ce(x^ x)
Image2890 f( X) = Xcn( x~xu)n dla wszystkich xe(a,b), to n=0
Image2905 x" , x2.xs b) ex = 2—= 1 + x + —+— + ... dla xeR „=0
EX4 v sinx = z (- i)" i-o (2k +1): ff=C”(R) f 2n+ i (0x) 2n+ i X = 0 (2n + l) • / &
Image2183 ex >1 +x, n>lnn, dla n = 1,2,....
Image239 f(tat) = f(tat + k?) dla & = 1,2, 3,...
Image240 y(s) = h(s) = G(s) ■ - = k 1 k s Ts+1 s (Ts+ l)s y(t) = h(t) = k ■ (1 - e T) dla u(t) = l(t
Image280 Podobnie jak dla sumatora pełnego, można wyznaczyć funkcje przełączające realizowane przez
Wieże Hanoi (2N) Dla N = 64 2N= 2“ = 18,450,000,000,000,000,000 Dysponując komputerem mogącym
Scan Pic0321 15. Funkcja e x czyli exp(-x) 15.1. Funkcja e~x dla zakresu O x <
Indukcja zupełna Korzystając z zasady indukcji matematycznej, wykazać, ze dla każdego n^N : 1) 1+3+5
Untitled 5 sinx^x — £x3 dla
więcej podobnych podstron