Image3165
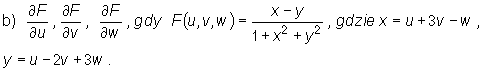
, s dF dF dF ^ i-f \ x-y , . .
b) ■=—,flay F(u)v)w) =-gdziex = u + 3v-w ,
dli dV dW \+XŁ + yŁ
y = u -2v +3w .
Wyszukiwarka
Podobne podstrony:
Image3165 , s dF dF dF ^ i-f x-y , . . b) ■=—,flay F(u)v)w) =-g
Image3022 df d ,1 /n „ - = —(-(2x-y)) = dX dX Z ytz traktujemy jako stale = —■ 2 = — Z z
Image3024 df_ = d_ az dz ~(2x-y)) = z x,y traktujemy jako stale /o w 1 , 2x-y = (2x-y)(--^) = -— ZŁ
Image3097 df _ 1 1 ^arctg^ dX yi + {Ł)2 1 Y X ^arctg* 0 9 ® J y ^arctg* 3f _ X f ^arctg* X2 + y2 e
Image3199 df, , — (x0Jo) dy ljm f(xo,yo + tł)-f(x0ly0) h-»0
Image3200 df, 1 ax
Image3446 dF dF ’df‘ 1 3un ć x_ dX dX dUj 1 1 dUn
Image3029 gratf = grad 1(2,5)(d[_ df) dx! dy xcos-yx2+y cosJx2 + y 9 xć +y ‘ 2-jx2 +y , a stąd ma my
Image3092 3F 3F du dv = df df dx1 dy dx dx du dv dy dy du dv 2e2xcosyJ-e2xsiny 2 u -
Image3117 ĆF df dx df dy x x3 ? - =--+--?-=QX+QX -3x dx dx dx dy dx
Image3451 badźgradF = df dx. ■ grad* .
df df dli dv • zwany jakobianem układu (*4.3), jest różny od zera dla. wszystkich par wartości u, v.
więcej podobnych podstron