Image3295
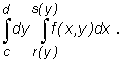
d s(y)
\ćy jf(xy)dx.
c r(y)
Wyszukiwarka
Podobne podstrony:
Image3288 d d J B(y)ćy = J sfyjf f(x,y)dx r(y)
Image3291 b q(x) jćx jf(x,y)ćy . a p(x)
Image3022 df d ,1 /n „ - = —(-(2x-y)) = dX dX Z ytz traktujemy jako stale = —■ 2 = — Z z
Image3029 gratf = grad 1(2,5)(d[_ df) dx! dy xcos-yx2+y cosJx2 + y 9 xć +y ‘ 2-jx2 +y , a stąd ma my
Image3289 t gM d J f(K y)dy M f(xY}óx .P(x) C r(y) / dy
>JF*W *6* S ^ *,6* w • xy nwoa 003N1N39I131NIiMaroud łNTELIGENTNEGO
P1000909 Inne właściwości iloczynu wektorowego aJ by cy ax K Cx r dx{jfxdj*=:S(3od)-e(aoB)
Image3294 f S{ /) f(x,y)dx r(y} ćy
ETNy5 2 I i D W ’ (*i ^ t h Xy)U + *3 Xę) - ~ U^tĄ^Ćy t ClJAC
Image3092 3F 3F du dv = df df dx1 dy dx dx du dv dy dy du dv 2e2xcosyJ-e2xsiny 2 u -
Image3097 df _ 1 1 ^arctg^ dX yi + {Ł)2 1 Y X ^arctg* 0 9 ® J y ^arctg* 3f _ X f ^arctg* X2 + y2 e
więcej podobnych podstron