Image408

sunięciu liczby odpowiednio o trzy i o jedną pozycję. Przetwarzanie wówczas sprowadza się do dodawania.
Przyjmujemy następujące oznaczenia:
J4, J3, J2, Ji — bity tetrady jednostek,
Z>4, D3, D2, Di— bity tetrady dziesiątek.
Konwersję BCD/BIN dla liczb BCD z zakresu (0)10 (99)10 można wówczas
symbolicznie przedstawić w następujący sposób:
|
Ją. J3 J2 Jl |
(xl) |
|
D3 D2 Di |
(x2) |
|
Di |
(x8) |
26 25 24 23 22 21 2°
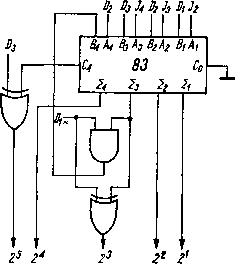
Przykładową implementację przetwornika BCD/BIN liczb z zakresu (0)10 -r--f- (63)10 przedstawia rys. 4.478.
BCD
_A_„
V V V V V V V
Dj D% Di J4 Jj Ą
2°
m
Rys. 4.478. Schemat logiczny równoległego przetwornika BCD/BIN liczb z zakresu (0)lo -f- (63)10
Przetwarzanie BIN/BCD przy użyciu sumatorów jest mniej efektywne. W celu przetworzenia należy dodać do siebie odpowiedniki BCD tych bitów liczby dwójkowej, które są równe jedynce.
Inną metodą konwersji równoległej jest metoda tablicowa, która może być zrealizowana najefektywniej przy wykorzystaniu półprzewodnikowej pamięci stałej. Słowo w kodzie wejściowym, np. w kodzie BIN, stanowi adres. Każdemu słowu adresowemu odpowiada słowo wyjściowe przedstawione w kodzie BCD. Załóżmy, że rozpatrujemy konwersję 10-bitowej liczby BIN. Do
Wyszukiwarka
Podobne podstrony:
ODPOWIEDZIALNOŚĆ CYWILNA • Lekarz wykonujący prywatną praktykę: Zobowiązuje się do leczenia
Umowa przedwstępna To umowa, w której jedna lub dwie strony zobowiązują się do zawarcia w przyszłośc
Istota strategii marketingowej sprowadza się do tworzenia odpowiedniej kompozycji poszczególnych ele
untitled Algorytmy LOOK i C-LOOK • Podobne do odpowiednio SCAN i C-SCAN. z tym że głowica przesuwa s
Trzy dni później. Cześć. Nie uczysz się do sprawdzianu ? Ojciec powiedział mi w tajemnicy, ze
Aktywność impresyjna sprowadza się do uczestnictwa dziecka w odpowiednio eksponowanych wartościach:
Projekt stanowi obraz tego co ma być wykonane względnie przetworzone, zaś proces projektowania sprow
CCF20100609�006 37. Analiza wrażliwości w progu rentowności sprowadza się do: • do
2.1 Pozycjonowanie Jak pamiętamy, pisanie w IAT^(u sprowadza się do układania treś
Image404 Konwersja liczby dwójkowej 1110100111 na równoważną jej liczbę dwójkowo-dziesiętną
Image4 Zakreśl poprawną odpowiedź. 1. Ryba jest żółta. 2. Dach jest zielony 3- £ To jest
image4 mini
więcej podobnych podstron