img028

28

3.1. Neurony

przy czyni współczynniki w,-, nazywane wagami synaptycznymi, mogą podlegać modyfikacjom w trakcie procesu uczenia, który stanowi jeden z zasadniczych wyróżników sieci neuronowych jako adaptacyjnych systemów przetwarzania informacji i o którym będzie dalej mowa w sposób znacznie bardziej szczegółowy. Element opisany przytoczonym wyżej równaniem liniowym jest między inymi zdolny do rozpoznawania wejściowych sygnałów.

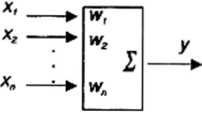
Aby to wyjaśnić, wystarczy zastosować notację wektorową. Niech zestaw sygnałów wejściowych neuronu tworzy wektor

zapisywany przez nas jako kolumna o » składowych. Wektor ten interpretować można także jako punkt w ?*-wy miarowej przestrzeni X, nazywanej przestrzenią wejść. Wektor ten (i inne wektory) zapisywać niekiedy będziemy w wygodniejszej postaci

X =< *i,*2.....sf» >⁷

gdzie T jest symbolem transpozycji. Nawiasy < oraz > w powyższym zapisie (a także w innych kontekstach dalej) używane są do grupowania uporządkowanych elementów - na przykład składowych wektora. Zestaw n współczynników wagowych także można rozpatrywać jako wektor

W =< I0|,U>2,. ...Wn >^T

wyznaczający punkt w n-wyniiarowej przestrzeni W, nazywanej przestrzenią wag. Przy tych założeniach równanie neuronu wyrazić można jako iloczyn skalarny wektora wejść i wektora wag:

y = W*X

Z formalnego punktu widzenia wygodniej będzie zastąpić iloczyn skalarny (zapisany wyżej z pomocą specjalnego operatora: gwiazdki *) zwykłym iloczynem transponowanego wektora W i wektora X

y = W^T X

Z ogólnie znanych właściwości iloczynu skalarnego wynika, źe sygnał wyjściowy neuronu y będzie tym większy, im bardziej położenie wektora wejściowego X w przestrzeni X przypominać będzie położenie wektora wag W w przestrzeni W. W ten sposób można powiedzieć,