img043

43

Rozdział 3. Liniowe sieci neuronowe

3.9 Uczenie z forsowaniem

Opisane wyżej techniki samo uczeni a (czy też , .uczenia bez nauczyciela”) mają bardzo interesującą odmianę, pozwalającą na wykorzystanie przytoczonych metod także w przypadku kiedy wektor wymaganych wartości sygnałów wyjściowych sieci Z^(;) jest znany (czyli w omawianym na samym początku zadaniu uczenia na podstawie ciągu uczącego U). Wszystkie omówione wyżej metody uczenia dadzą się wtedy bardzo efektywnie zastosować przy zastosowaniu prostej zamiany odpowiednich y przez stosowne z. Takie uczenie ma charakter „forsowania” poprawnych rozwiązań bez względu na to, co robi sieć. Metoda taka może mieć niekiedy istotną przewagę nad metodą DELTA, ponieważ nie wymaga w sposób jawny wyliczania wartości błędów popełnianych przez neurony sieci, co może bardzo istotnie przyspieszyć proces uczenia. Ponieważ istnieje głęboka i łatwa do prześledzenia analogia omawianych metod „forsownego uczenia z nauczycielem” do dyskutowanych wyżej metod „uczenia bez nauczyciela”— ograniczymy się jedynie do przytoczenia odpowiednich wzorów, pomijając tym razem dyskusję i próby interpretacji tych wzorów. Wyróżnić przy tym można następujące metody:

- metoda autoasocjacji: - metoda przyrostowej autoasocjacji:

(»*

^Ki+" = u{.....[<*;•» -- 4{-")]

- metoda zbliżania wektora wag do wektora odpowiedzi:

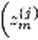
Wprowadzając podobnie jak wyżej oznaczenie iti) -

I 0 w przeciwnym przypadku

oraz korzystając z wprowadzonej wyżej definicji możemy podać kolejne trzy dalsze reguły uczenia:

_M(m    _    „,(■”><) > ₊    1)

w\^m W+'¹ = w-5” ’^H:1 + V - 1 )(2i«J - 1)

Wybór jednej z podanych wyżej możliwości podyktowany być musi każdorazowo oceną ich przydatności w konkretnym zadaniu, przy czyni z powodu braku ogólnej teorii konieczne są eksperymenty i poszukiwania oparte na badaniach empirycznych.

Hola „forsownego uczenia” może być dokładniej prześledzona dla dwóch interesujących teoretycznie i przydatnych praktycznie konkretnych sytuacji. Przepiszmy równanie autoa-socjacji z podanej wyżej formy skalarnej

UJ i    — “•'»    ' V * i *m