img054

54

4.3. Właściwości nieliniowych sieci wielowarstwowych

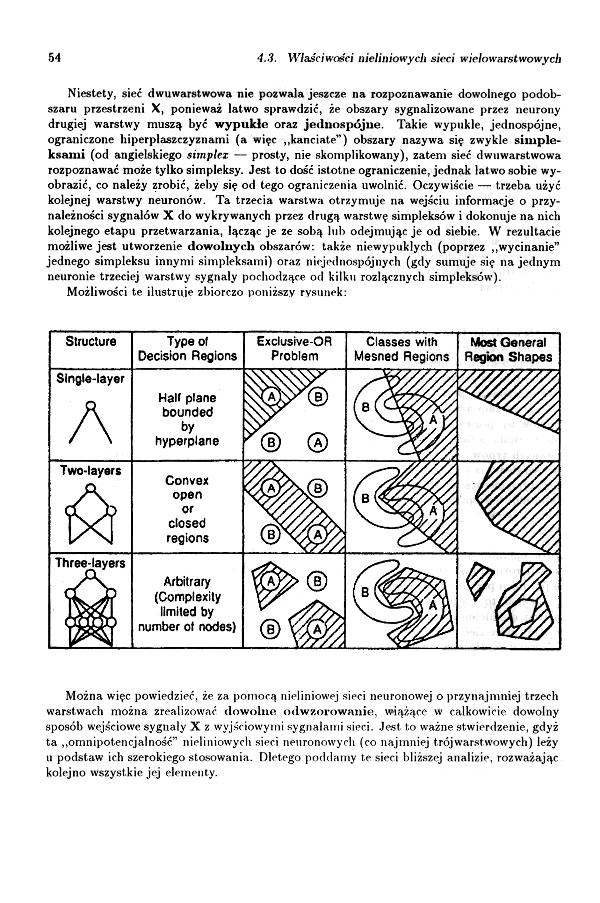
Niestety, sieć dwuwarstwowa nie pozwala jeszcze na rozpoznawanie dowolnego podob-szaru przestrzeni X, ponieważ łatwo sprawdzić, że obszary sygnalizowane przez neurony drugiej warstwy muszą być wypukłe oraz jednospcSjue. Takie wypukłe, jednospójne, ograniczone hiperplaszezyznami (a więc „kanciate”) obszary nazywa się zwykle simpleksami (od angielskiego simplcz — prosty, nie skomplikowany), zatem sieć dwuwarstwowa rozpoznawać może tylko simpleksy. Jest to dość istotne ograniczenie, jednak łatwo sobie wyobrazić, co należy zrobić, żeby się od tego ograniczenia uwolnić. Oczywiście — trzeba użyć kolejnej warstwy neuronów. Ta trzecia warstwa otrzymuje na wejściu informacje o przynależności sygnałów X do wykrywanych przez drugą warstwę simpleksów i dokonuje na nich kolejnego etapu przetwarzania, łącząc je ze sobą lub odejmując je od siebie. W rezultacie możliwe jest utworzenie dowolnych obszarów: także niewypuklych (poprzez ,,wycinanie” jednego simpleksu innymi simpleksami) oraz niejrdnnspójnych (gdy sumuje się na jednym neuronie trzeciej warstwy sygnały pochodzące od kilku rozłącznych simpleksów).

Możliwości te ilustruje zbiorczo poniższy rysunek:

Structure	Type of Decision Regions	Exclusive-OR Problem	Classes with Most General Mesned Regions Region Shapes
Slngle-layer A	Hall piane bounded by hyperplane		Am.
Two-layers A	Convex open or closed regions		i§§| H§
	Arbitrary (Complexily llmited by number ot nodes)	®ml

Można więc powiedzieć, że za pomocą nieliniowej sieci neuronowej o przynajmniej trzech warstwach można zrealizować dowolno odwzorowanie, wiążące w całkowicie dowolny sposób wejściowe sygnały X z wyjściowymi sygnałami sieci. Jest to ważne stwierdzenie, gdyż ta ,,omnipotencjalność” nieliniowych sieci neuronowych (co najmniej trój warstwowych) leży u podstaw ich szerokiego stosowania. Dletego poddamy te sieci bliższej analizie, rozważając kolejno wszystkie jej elementy.