img055

55

Rozdział 4. Nieliniowe sieci neuronowe

4.4 Formy nieliniowości neuronu

Funkcja wiążąca łączne pobudzenie neuronu e z jego sygnałem wyjściowym y

y - V (0

opisana wyżej jako funkcja progowa, miewa także liczne modyfikacje, z których na szczególną uwagę zasługuje sigmoidalna funkcja wywodząca się z funkcji logistycznej

_ 1 ^V ~ 1 + exp (- fSc)

Zaletą tej funkcji jest prosta i łatwa do obliczenia wartość jej pochodnej. Łatwo wykazać, że w przypadku funkcji logistycznej z czego będziemy dalej w sposób istotny korzystali.

Na marginesie tej dyskusji warto odnotować fakt, że w literaturze spotyka się różne oznaczenia funkcji <p(e) i jej parametrów. Ilustruje to rysunek pokazujący przebieg funkcji logistycznej dla dwóch wartości parametru 3, zaczerpnięty z książki [Hech90], na którym — zgodnie z tradycją literatury anglojęzycznej — sumaryczne pobudzenie e oznaczono jako nełj, 3 oznaczono jako 0n a parametr Oj odpowiada w notacji przyjętej w tej książce wartości wyrazu wolnego w₀.

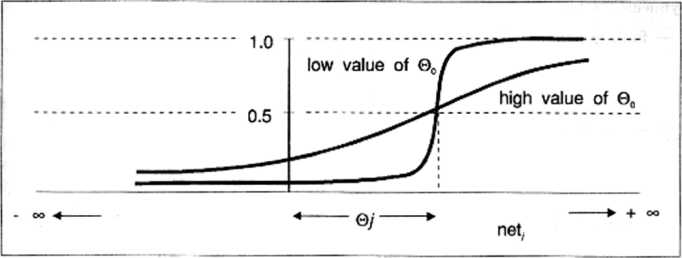
Ważną właściwością funkcji logistycznej jest fakt, że zbiór jej wartości należy do otwartego zbioru y € (0, 1), co oznacza, że wartości 0 i 1. mające istotne znaczenie przy niektórych interpretacjach funkcjonowania*sieci nauronowych (np. teoria tzw. sieci logiki ciągłej, por. [TadeOla]) są tu nieosiągalne. Z tego względu mimo niewątpliwych zalet funkcji siguioidalnej (logistycznej) rozważane są także inne funkcje opisujące nieliniową zależność między sumarycznym pobudzeniem, a sygnałem wyjściowym neuronu. Przykładowo, chętnie stosowaną funkcją jest tangens hiperboliezuy

y — tanh ((ic)