img057

57
Rozdział 4. Nieliniowo sieci neuronowe
— funkję BSB (Rratn Siatę in a Box):
V =
1 gdy e > 1 e gdy I >0-1 -1 gdy e < -1
— funkcję SPR (Spaito-Temporal Patiem Recognition)
+ A oti/j) + fi e+J
gdzie „funkcja ataku” A[.] definiowana jest w sposób następujący:
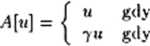
« > 0 u < 0
a zapis e+ oznacza nieujemną wartość e:
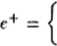
e gdy e > 0 0 gdy p. < 0
Podane wyżej funkcje wywodzą się głównie z publikacji inżynierów stosujących sieci neuronowe jako wygodne nowoczesne narzędzia przetwarzania informacji i poszukujących takich form opisu elementarnego procesora (jakim jest dla nich neuron), które pozwalają na wygodną analizę matematyczną zachodzących zjawisk (sigmoida), łatwą realizację techniczną (perceptron) lub wygodne modelowanie w formie programu symulacyjnego (signum). Tymczasem odmienne formy nieliniowości rozważają neurofizjologowie zajmujący się opisem neuronu jako obiektu biologicznego będącego przedmiotem ich badań. Tutaj chętnie stosuje się w różnych kontekstach funkcję logarytmiczną (nawiązującą do znanego prawa Webera — Fechnera). Oczywiście t.ę listę można by dowolnie wydłużać.
4.5 Uczenie nieliniowego neuronu
Rozważmy problem uczenia nieliniowych sieci neuronowych. Dla uproszczenia przyjmijmy, że analizować będziemy wyłącznie regułę DELTA w jej podstawowej postaci. Wzór opisujący zmianę wartości składowych wektora wag podczas prezentacji próbek z ciągu uczącego
U = « >,< X(2\*'2) »
wygodnie będzie wyprowadzić początkowo dla jednego neuronu. Formuły uczenia szukać będziemy opierając się na wprowadzonej wyżej (przy rozważaniu sieci Adaline i Madaline) regule minimalizacji funkcjonału błędu średniokwadratowego:
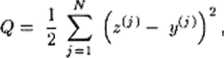
gdzie oczywiście
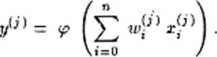
Wyszukiwarka
Podobne podstrony:
img057 57 Rozdział 4. Nieliniowo sieci neuronowe — funkję BSB (Rratn Siatę in a Box): V = 1 gdy e &g
Sieci CP str057 57 Rozdzia.1 4. Nieliniowe sieci neuronowe — funkję BSB (Rrain State in a Uoz): 1 gd
Sieci CP str057 57 Rozdzia.1 4. Nieliniowe sieci neuronowe — funkję BSB (Rrain State in a Uoz): 1 gd
img063 63 Rozdział A. Nieliniowe sieci neuronowe klasycznej metody backpropagalion z wykorzyslniem e
img053 53 Rozdział 4. Nieliniowe sieci neuronowe podział ten formuje granica mająca postać hiperplas
img055 55 Rozdział 4. Nieliniowe sieci neuronowe4.4 Formy nieliniowości neuronu Funkcja wiążąca łącz
img059 59 Rozdział 4. Nieliniowe sieci neuronowe4.6 Uczenie sieci nieliniowej Opisany wyżej algorytm
img061 61 Rozdział 4. Nieliniowe sieci neuronowe Na samym początku wyznacza się zatem poprawki fila
img063 63 Rozdział A. Nieliniowe sieci neuronowe klasycznej metody backpropagalion z wykorzyslniem e
Sieci CP str059 59 Rozdział 4, Nieliniowe sieci neuronowe4.6 Uczenie sieci nieliniowej Opinany wyżej
więcej podobnych podstron