img061

61

Rozdział 4. Nieliniowe sieci neuronowe

Na samym początku wyznacza się zatem poprawki fila neuronów stanowiących wyjściową warstwę sieci (ni €    Tu sprawa jest prosta, ponieważ dla poszczególnych sygnałów

\Jm istnieją w ciągu uczącym wzorcowe (oczekiwane) wartości Zm\ z którymi można je porównywać, wyznaczając bezpośrednio błąd Zakładamy przy tym dla prostoty, że numeracja składowych wektora wzorców jest identyczna z numeracją neuronów tworzących wyjściową wastwę sieci (tylko przy zachowaniu tego warunku m w i m w mogą być utożsamiane!). Wówczas

A*™” =

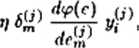
gdzie dla m 6

₆0 ) ₌ Jf) _

^vm ~rn

Wzór ten dla m € w postaci

OT

_y oraz dla <p(c) w postaci funkcji logistycznej zapisany może być

A"’!"”"’ = V f^» - £’) (I - £>)

dogodnej do praktycznych obliczeń.

Na razie wprowadzane wzory nie wnoszą istotnej nowości; ich zapis jest. trochę bardziej złożony (przez konieczność uwzględniania numerów m), jednak icli ogólna struktura jest identyczna z wcześniej wprowadzonymi wzorami opisującymi proces uczenia dla pojedynczego neuronu. Jednak z chwilą skoncentrowania uwagi na neuronach warstw ukrytych sytuacja się zmienia. Można bowiem przez analogię zapisać także dla tycli neuronów regułę

A«!^mW'=

‘MO o)

ii)

jednak dla m € 9Jl_u nie ma możliwości bezpośredniego określenia wartości S„^}, *. Rozważmy jednak zbiór    Zgodnie z wprowadzonymi oznaczeniami jest to zbiór neuronów, do

których dociera sygnał j/m* czyli sygnał wyjściowy z rozważanego neuronu warstwy ukrytej. Załóżmy na chwilę, że Mo C M_y% to znaczy załóżmy, że rozważany neuron należy wprawdzie do warstwy ukrytej, ale jego sygnał wyjściowy dociera wyłącznie do neuronów warstwy wyjściowej, czyli tych, dla których wartości błędów mogą być bez trudu określone. Przy tym założeniu można wykazać [Rume86], że błąd s!,^J,^> neuronu warstwy ukrytej może być obliczony poprzez wsteczne rzutowanie (czyli barkprttpngałion) błędów wykrytych w warstwie odbierającej sygnały:

«» = £ "fi™ 4°

*€®t*

Warto zwrócić uwagę na współczynniki wagowe, wykorzystywane przy wstecznym rzutowaniu błędów. Czynnik    należy rozumieć jako wagę występującą w neuronie o numerze

k przy jego wejściu numerze m, czyli odbierającym sygnał od aktualnie rozważanego neuronu. Oznacza to, że rzutowane wstecznie błędy mnożone są przez te same współczynniki, przez które mnożone były przesyłane sygnały, tyle tylko, że kierunek przesyłania informacji zostaje w tym wypadku odwrócony: zamiast od wejścia do wyjścia przesyła się je od wyjścia kolejno w kierunku wejścia.

Stosując opisaną wyżej technikę wstecznej propagacji błędów można nauczyć całą sieć, ponieważ każdy neuron warstwy ukrytej albo znajduje się w przedostatniej warstwie sieci