img058

58

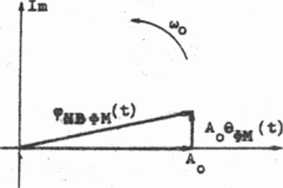
Rys. 1.14. Mykres wskazowy wąskopasmowej modulacji kąta fazowego NB9M

Rysunek 1.14 może nas wprowadzić w błąd - wynika z niego przecież, 2e amplituda sygnału NB§M wykasuje niewielkie zmiany, co teoretycznie nie jest możliwe. Jest to jednak tylko niedoskonałość rysunku, na którym nie uwzględniono pozostałych, bardzo małych, składowych sygnału NBłM*.

Widmo gęstości mocy sygnału NB#M znajdujemy przy założeniu, że sygnał modulujący jest deterministycznym sygnałem energii x(t)'*“*- X(co), korzystając z określenia (1.2.40) oraz właściwości (A-13b) przekształcenia Fouriera**. Transformata odchyłki kąta fazowego dla modulacji fazy jest równa

(1.2.42a)

S^:{8_pM(t)} = k_pMX(m>)

zaś dla modulacji częstotliwości na mocy twierdzenia (A-17) wynosi

(1.2.42b)

{e_FM(t)}

k ^

^KFM jw

•Jeżeli sygnał NEffM będziemy jednak wytwarzać zgodnie z aproksymacją (1.2.40) jako złożenie sygnału dwuwstęgowej modulacji amplitudy i sygnału nośnego (co jest praktyką), to amplituda sygnału wypadkowego będzie istotnie wykazywać pewne wahania. Efekt ten można wyeliminować za pomocą ogranicznika amplitudy.

**. Dotychczas zakładaliśmy, że sygnał modulujący jest stacjonarnym procesem losowym. Jednakże przyjęcie takiego założenia w przypadku modulacji NBFM czyni zadanie wyznaczenie jej widma praktycznie niewykonalnym,

t

gdyż proces losowy ‘PnBFM^*^ * k_fM j x(t)dt jest niestacjonarny.