img062

62

5. Metody wzorców

*1

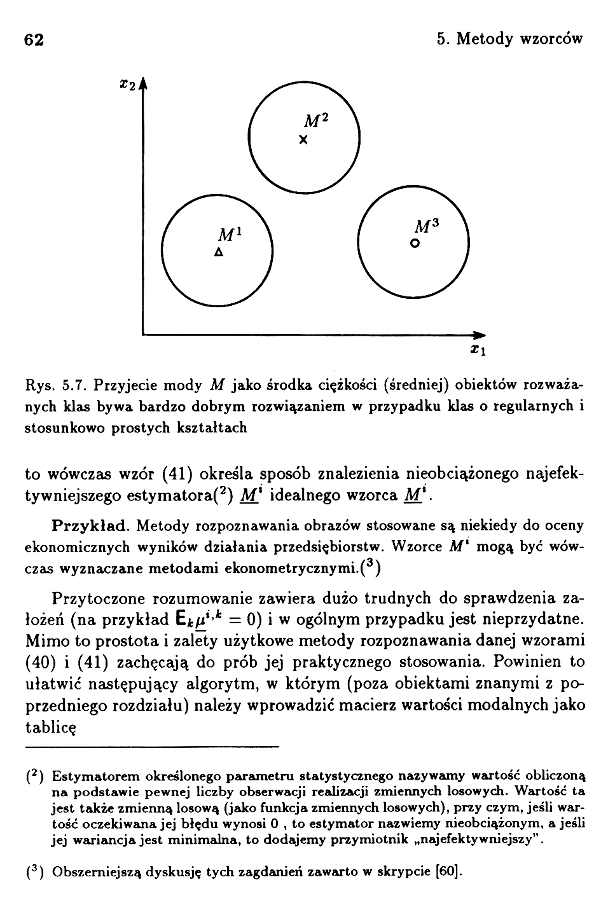
Rys. 5.7. Przyjęcie mody M jako środka ciężkości (średniej) obiektów rozważanych klas bywa bardzo dobrym rozwiązaniem w przypadku klas o regularnych i stosunkowo prostych kształtach

to wówczas wzór (41) określa sposób znalezienia nieobciążonego najefektywniejszego estymatora(²) A£* idealnego wzorca M*.

Przykład. Metody rozpoznawania obrazów stosowane są niekiedy do oceny ekonomicznych wyników działania przedsiębiorstw. Wzorce A/‘ mogą być wówczas wyznaczane metodami ekonometrycznymi.(³)

Przytoczone rozumowanie zawiera dużo trudnych do sprawdzenia założeń (na przykład E*/x^,,ł = 0) i w ogólnym przypadku jest nieprzydatne. Mimo to prostota i zalety użytkowe metody rozpoznawania danej wzorami (40) i (41) zachęcają do prób jej praktycznego stosowania. Powinien to ułatwić następujący algorytm, w którym (poza obiektami znanymi z poprzedniego rozdziału) należy wprowadzić macierz wartości modalnych jako tablicę

(²)    Estymatorem określonego parametru statystycznego nazywamy wartość obliczoną na podstawie pewnej liczby obserwacji realizacji zmiennych losowych. Wartość ta jest także zmienną losową (jako funkcja zmiennych losowych), przy czym, jeśli wartość oczekiwana jej błędu wynosi 0 , to estymator nazwiemy nieobciążonym, a jeśli jej wariancja jest minimalna, to dodajemy przymiotnik „najefektywniejszy”.

(³)    Obszerniejszą dyskusję tych zagdanień zawarto w skrypcie (60).