img071

• • •

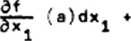
nazywamy różniczkę zupełny, albo krótko różniczkę, funkcji ⁴ w pun*-etę a. Oznaczamy ję przez df(a).

3est oczywiste, że Jeśli funkcja f Jest różniczkowałoś w ounkcie a to ma ona w tym punkcie różniczkę zupełnę oraz

(6.6

f(a*h) ■ f(a) ♦ df{8) ♦ £{h) .Ihl , lim £(h) * o

IhlrO

n

'zobacz definicję 5.3 oraz wniosek z definicji 5.6'*.

»V tym przypadku wzór (6.6) może więc służyć do obliczania wartości przybliżonych ffę+h), gdy znamy wartości funkcji f i jej pochodnych cząstkowych w punkcie a oraz ! hI_n Jest na tyle małe, iż możemy zaniedbać składnik £(h) ,|hl_n, Koócowa część ostatniego zdania nie jest precyzyjna. Fakt, że "Jakoś wielkość Jest ne tyle mała, iż można pominąć przy obliczeniach pewien składnik" zależy od dokładności z Jakę chcemy, a raczej z Jakę pragniemy uzyskać wartość f(a*h). Miarę błędu bezwzględnego przybliżenia f'a*h' wyznaczonego poprzez wartość f(a) ♦

♦    df(a) Jest liczba lfc(h)l.lhl_n, którę w konkretnych zadaniacn trudno wyznaczyć, a nawet sensownie oszacować z góry. Niemniej Jednak, w pewnych przypadkach stosowanie różniczki zupełnej do obliczania wartości funkcji daje wyniki, które mogę zadowolić nawet wymagających odbiorców oblicze*, świadczy o tym następujęcy

Przykład

Niech f:R² 3 (x,y) — xy, a • («₁#«₂) *    ^h * ^j»^h2    *

*    10,002;0,004). Wówczas f(e) ♦ df(a) - 6 * 2 0,002 ♦ 3 0,004 -

■ 6,016, a f(a+h) • 6,016008. Wartości te różnię się więc dopiero na szóstym miejscu po przecinku.

Twierdzenie 6.3. Niech F:R^P DK(b,t) 3 (u^, ... ,u_p; —*R oraz f l_<:RⁿD K{a,r) 3 (x7,•••,x_n) —w R (k » l,...,p;. Zakłademy, że funkcja f Jest różniczkowałoś w punkcie a> funkcje f^ k » l,...,n) zaś niecn będę różniczkowalne w punkcie b * (fa) , • • •,f_p(a)) . wówczas, jeśli g jest funkcję złożonę określonę wzorem

g(x) ■ F(f _t(x).....^fp(*))

to

dg(a) . df'f₁.....f_p)(a)

Twierdzenie 6.3 mówi więc, że przy pewnych założeniach wartość roz

niczki zupełnej nie zależy od tego czy zmienne u^.....u sę niezależne

czy też sę funkcjami innych zmiennych niezalożnych.

Dowód twierdzenia 6.3. Niech u^ ■ f_k(x^,... ,x_n) . Wówczas ko-