img072

72

Znajdziemy teraz postać widma gęstości mocy tonowej modulacji częstotliwości dla dużych wartości dewiacji fazy    1. Zgodnie z przepi

sami (1.2.45) oraz (1.2.46) należy najpierw określić rozkład prawdopodobieństwa g(v) wartości znormalizowanego harmonicznego sygnału modulującego v(t) * sin o>_mt, rys. 1.26.

Poszukiwane prawdopodobieństwo g(v) Av = Pr { v<v(t) < v + 4v| określimy w sposób geometryczny

_/..x ...    « ^Tv arcsin( v + Av) - arcsin v

g(v; Av * z y— = z    t...-

¹    1 ®n

g(v) = i lim arcsin(v ♦ Av) - arcsin v _a * Av — 0    ^Av

_ 1 darcsin v _    1_

' * ?v    ,-f

*7l - \r^l

|vt < 1

Znajęc funkcję rozkładu wartości g(v) dla sygnału harmonicznego możemy, korzystając z zależności (1.2.47), wyznaczyć widmo gęstości mocy szerokopasmowej tonowej modulacji częstotliwości

_A2

⁵wbfm^(m) * i ......¹ ......... -    ..... ¹ ...... 1 ^<1-²-“⁾

• & ^ CU - (w+ CO_Q ) ²    *6." O) - (co- „₀>²’

Widmo (1.2.66) jest przedstawione na rysunku 1.21. Pamiętajmy jednakże o tym, że jest to tylko aproksymacja (dla dużych wartości A(pp_M). Wyniki dokładnej analizy widmowej pokazane są na rysunku 1.18. Stwierdzamy istot ne podobieństwo otrzymanych wyników, szczególnie dla    ^s 15.

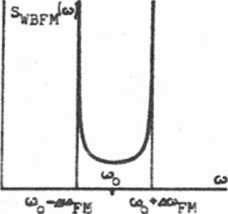
Rys. 1.21. Widmo gęstości mocy tonowej szerokopasmowej modulacji czę stotliwości WBFH