img081

81

Uśredniamy po czasie

<R_X (t+fvt7> ¹ R_x(«) <4_t (t^T)rf_T (t)>

8 0 0

<^_T (t+r)rfy (t)> Jest funkcją korelacji własnej okresowego sygnału oo    «

&    (t); korzystając z CC-26a), wiersza 5 tabeli A-l oraz trygonometrycz-

o

nej postaci szeregu Fouriera (A-2) otrzymujemy

< 3r (t+z)óT (t)> 0 0			cosl UJ T «»■«—n o Tz
u o 3	0		0

‘ 6(u>- lu>₀) l*-oo

(1.3.2)

Uśredniona po czasie funkcja korelacji własnej sygnału spróbkowanego równa się więc

(t+ę,t)> = R (xr) (1¹2 } coslw.t)

⁸    rl

o    1¹1

a odpowiadające jej widmo gęstości mocy, właściwość (A-13b)

S_y (to) s

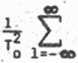
S_x(o>- lw₀)

(1.3.3)

Stwierdzamy, że widmo sygnału spróbkowanego Jest ciągiem widm sygnału oryginalnego przesuniętych o wielokrotność częstotliwości próbkowania ^wo ^{= 2ir/T}o» ^{rys1 1}’^2Ą1

Na rysunku 1.24a przedstawiono przypadek, gdy częstotliwość próbkowania o>₀ jest dokładnie równa częstotliwości Nyquista 2«»>g. Widzimy, te przepuszczając sygnał spróbkowany przez idealny filtr dolnoprzepustowy ■oźerny odtworzyć sygnał oryginalny¹. Odtworzenie sygnału oryginalnego jest możliwe także, gdy częstotliwość próbkowania jest większa od czę-

1

2 całą pewnością widmo gęstości mocy sygnału wyjściowego filtru jest równe widmu gęstości mocy sygnału oryginalnego. Oznacza to Jednakże tylko tyle, że proces wyjściowy filtru jest równy procesowi wejściowemu w sensie statystycznym, a nie tożsamościowym £ 10].