img087tc1

Egzamin z teorii miary i całki. Semestr IV. Rok ak. 2006/07.

Zadanie 1.

(a)    Proszę podać definicję cr-algebry.

(b)    Czy rodzina T C 2ⁿ jest cr-algebrą, gdzie H = (xi, x₂, x₃, x₄, Xs} oraz T = (12,0, {Xl}, {xi,X₂}, {xi,X₂,X₃}, {xi,X₂,X₃,X₄}, {x₂, X₃, X₄, X₅}}? Odpowiedź proszę uzasadnić.

(c) Wyznaczyć cr((—2,2], (2,3)) C 2^S.

Zadanie 2.

(a)    Proszę podać definicję miary.

(b)    Niech M. będzie cr-algebrą wszystkich podzbiorów zbioru X i niech xo € X. Wykazać, że wzór:

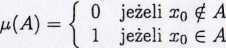
określa miarę.

Zadanie 3.

(a)    Proszę podać definicję całki Lebesgue’a.

(b)    Obliczyć następujące całki Lebesgue’a:

-    /_R_ (3xi-3,7) (z) + 5X[2,4] (x))dx,

-    Jj__{5 5}j sgn(—x³ + 2x² + 2x — 4)dx.

Zadanie 4.

(a) Proszę sformułować twierdzenie Lebesgue’a o zbieżności zmajoryzowanej

(ograniczonej).

(b) Proszę uzasadnić, że ciąg

f    dla x e [0, n)

0    dla x > 2n

fn{x) = < -^r + £ dla x 6 [n, 2n)

nie spełnia tezy tego twierdzenia.