img096

66

66

h + ^L2 "

*1 . x₁ ♦ Lp . x₂

bilene masowy L„ • x„ bilene wodny

Wilgotność bezwzględne mieszaniny x_ff będzie równe I*- • X- 4 Lp • x₂

x_B »    +" Łpsuobego powietrza

Zekłalasy* że komora mieszania jest izolowana, czyli nie tracimy ani nie doprowadzamy ciepła, to wówczas bilans cieplny procesu będzie następujący:

^L1 * *1 * h * *2 " \ • ⁱm

Entalpie mieszaniny będzie równe

4    _

^m

i ^ + Lp # ip

T^-rr;-

kJ/<1+x)kg

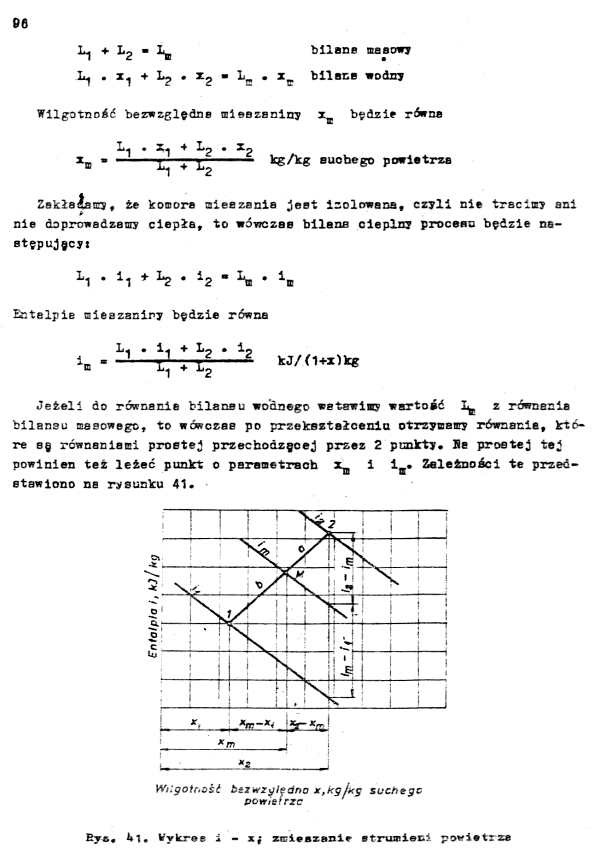
Jeżeli do równanie bilansu wodnego wstawiwy wartość 1^, z równania bilansu masowego, to wówczas po przekształcenia otrzymamy równania, które s§ równaniami prostej przecfaodzęoej przez 2 punkty# He prostej tej powinien też leżeć punkt o parametrach    i i_B# Zależności te przed

stawiono na rysunku 41.

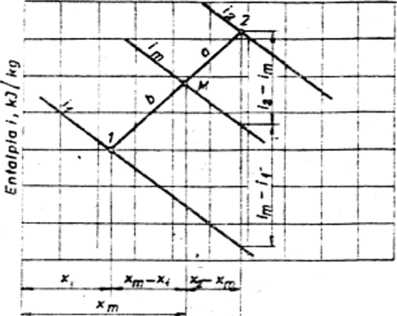
Witgotnoić bezwzględno x,*g!«s suchego powietrze

u--*1---J

By*. **1. Vykree

xf zmieszanie itruaietf powietrze