img106

106

8.4. Uczenie sieci BAM i przykład jej działania

8*4 Uczenie sieci BAM i przykład jej działania

Uczenie sieci BAM podlega prawu Hebba przy współczynniku ij = 1, zatem po pokazaniu w ciągu uczącym pary sygnałów < X^(k\Y<^k) > macierz wag W zostaje zmodyfikowana o składnik będący macierzą korelacji X<^ł) i Y^^ł).

yp(*+») -    - W⁽-^k) + Y^^kYr

Po przeprowadzeniu procesu uczenia od początku do końca mamy więc następujący stan pamięci sieci

W =    *^w<k)

fc=i

(oczywiście przy założeniu    =0).

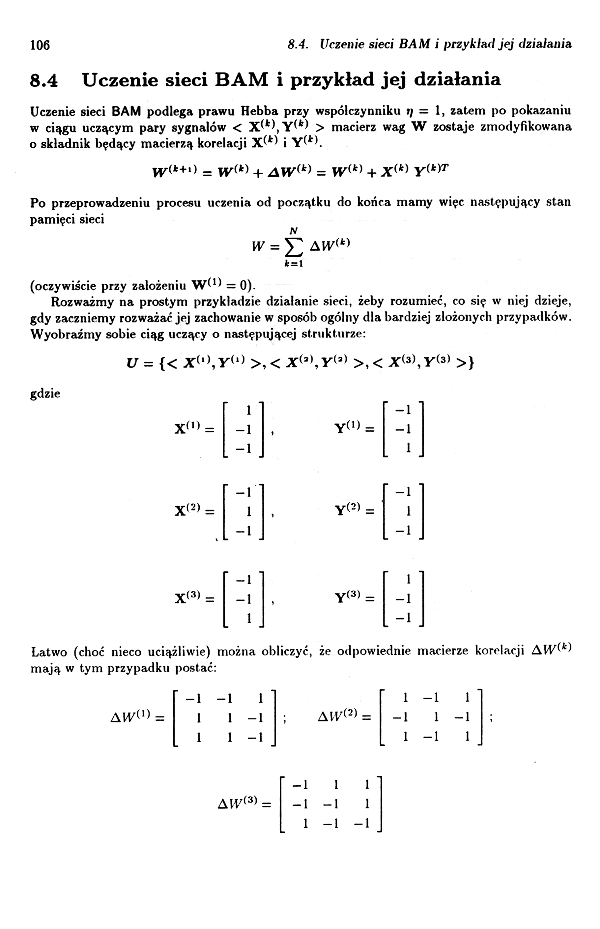
Rozważmy na prostym przykładzie działanie sieci, żeby rozumieć, co się w niej dzieje, gdy zaczniemy rozważać jej zachowanie w sposób ogólny dla bardziej złożonych przypadków. Wyobraźmy sobie ciąg uczący o następigącej strukturze:

U = {<    >,< X⁽³⁾,Y<³⁾ >,< X<³\Y<^s) >}

	1 ■		' -1 '
x^f,> =	-1	, Y<‘> =	-1
	-1		1
X® =	' -1 1	y(2> =	‘ -1 ' 1
*	-1		-1
	-1 '		1 '
x<^3> =	-1	Y<^3> =	-1
	1		-I

Łatwo (choć nieco uciążliwie) można obliczyć, że odpowiednie macierze korelacji mają w tym przypadku postać:

	-i-i r		i -i i'
A WM =	i i -i	ii u	-i i -i
	i i -i		! -! 1
		■ -i i i
AW^(3) =		-i -i i
		l—i—i