img109

109

jemy również, że g(a) * O oraz, że £    (e)J² ♦ ,,, ♦ £|S- (a)j²>0.

Nic zmniejszając ogólności rozważać, możemy założyć, że ^2— (a) $ 0.

^axn

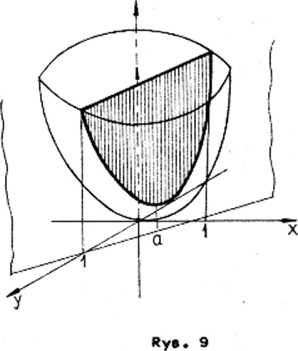
Wówczas na podstawie twierdzenia o funkcji uwikłanej (twierdzenie 6,4) warunek (9,7) możemy zaóiaać w postaci x_n • u(xj,..,»x_n_, A zatem zagadnienie znalezienia ekstremum funkcji f przy warunku (9,7) sprowadza się do wyznaczenia ekstremum lokalnego funkcji n-l zmiennych:

F(x,

-W

f(x₁T....X_n.₁fU(x₁,

*n-l»

du

Oeśli więc punkt a ■ (a^, gdzie a_n * u(a^*•.,#*_n_₁) jest punktem ekstremum warunkowego funkcji f przy warunku(9,7), to punkt a' ■

• (Sj,*•. .^an-j) Jest punktem ekstremum lokalnego funkcji F i na odwrót Dlatego powinny być spełnione równania

ÓF

^7

(a')

O dla i

^an>

.n-i

lub inaczej (zobacz wzór (6.4) ne pochodnę częatkowę funkcji złożonej)

3*1

. df

(a')

df

•K-

(a) ♦

(a)

du

(a') (i • 1,..,n-l)

Pochodna •rr—- (a') możemy wyznaczyć na podstawie twierdzenia 6,5. ^OKi

ściślej mówięc, korzystamy ze wzoru (6.8) na pochodnę częatkowę funkcji uwikłanej i otrzymujemy

du

W rezultacie

(a')

"31

(i * 1,

,n-l)

n

(a)

,n-l)

(i- 1,

skęd

1 (9,8)