img198

198

konwekcje swobodne

f (.

c, / , g» V, ^t)

gdzie* w - prędkość przepływu,

1 - char/tł trry etyczny wymiar liniowy, na przykład średnioe rury, A. - współczynnik przewcćżenia ciepła,

c - ciepło właściwe, f - gęstość,

\? - współczynnik lepkości kin/ma tycznej,

g - przyspieszenie grawitacyjne,

p - współczynnik rozszerzalności objętościowej,

At - różnica pomiędzy temperaturę powierzchni ściany i tempera-

/ turę opływejęcego tę powierzchnię gezu lub cieczy, Doświadczalne wyznaczenie wartości cc « zależności od tak znacznej ilości parametrów, i to w szerokim zakresie zmiany ich wartości, oraz dla różnych ukłaców geometrycznych byłoby niezmiernie trudne. Korzysta-jęc z teorii podobieństwa, której celem jest przenoszenie wyników doświadczalnych ne zjawieke podobne, nożne uatelić uogólnione zależności funkcyjne, ważne dla wszystkich przypadków podobnych. Teorię podobieństwa możne stosować do dowolnych zjawisk fizycznych, jeżeli sę znane warunki podobieństwa tych zjowisk. W zjawlBkach podobnych można porównywać ze sobę tylko wielkości jednorodne i tylko w odpowiadajęcych sobie punktach układu i chwilach. Jednorodnymi wielkościami nazywamy takie, które posiadaję jednakowe znaczenia fizyczne i toki sam wymiar.

W zjawiskach podobnych spełnione sę następujące warunki*

a) podobieństwo geometryczne układów

- L. - —

3 z

Układy sę geometrycznie podobne, jeżeli stosunki wymiarów liniowych we wszystkich kierunkach maję stałę wartość Cj., zwsnę atałę podobieństwa geometrycznego;

b) podobieństwo wszystkich parametrów charakteryzujęcycb dane zjawisko. W przypadku konwekcji wymuszonej musi istnieć podobieństwo na-stępujęcycb parametrów*

JL

V

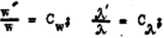
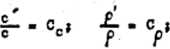
c

V

Wartośói stałych podobieństwa C_w, C^, C₀, Cp, nie muszę być jednakowe i przeważnie keżda z nich posiada innę wartość;

c) liczby podobieństwa maję jednakowe wartości. Liozby podobieństwa sę to bezwymiarowe wyrażenia zawierajęce wielkości charakterystyczne