Cwicz 4 2

gdzie L - długość rury [m], d - średnica wewnętrzna rury [m], u - średnia liniowa prędkość przepływu płynu [m/s], p - gęstość płynu [kg/m³].

Współczynnik X nazywa się współczynnikiem oporów przepływu lub współczynnikiem tarcia. Dla przepływu laminarnegoprzewodem o przekroju kołowym, współczynnik oporów przepływu wynosi 64/Re. Wynika to z teorii przepływu laminamego. Dla przepływu burzliwego współczynnik oporów przepływu jest także funkcją liczby Reynoldsa a ponadto zalety od szorstkości (chropowatości) rury. W literaturze fachowej podawane są liczne równania empiryczne umożliwiające obliczenie współczynnika X dla przepływu burzliwego. Są to równania o ogólnej postaci

(4.4)

b

= a

Re^m

gdzie a, b i m są stałymi doświadczalnymi dla określonego zakresu liczb Reynoldsa.

Do najbardziej znanych nalety równanie Blasiusa dla rur gładkich, obowiązujące dla 3-10³< Re < MO⁵

(4.5)

(4.6)

₌ 0,3164

Re⁰-²⁵

Liczba Reynoldsa zdefiniowana jest równaniem

Re = iLŚ-2.

Tl

gdzie ą- lepkość płynu [Pa s].

Wpływ szorstkości ścianek rury na wielkość współczynnika oporów przepływu X jest pokazany na rysunku 4.1. Przedstawiony wykres sporządzony jest w układzie dwulogarytmicznym. Na rysunku tym szorstkość określona jest stosunkiem k/d czyli wysokości występów na Ściance (stanowiących o jej szorstkości) do średnicy ruty. Widoczne jest, że dla rur o dużej szorstkości w zakresie dutych wartości liczby Reynoldsa, współczynnik oporów przepływu zalety głównie od szorstkości ścianek, a o oporach przepływu decyduje prędkość przepływu i gęstość płynu.

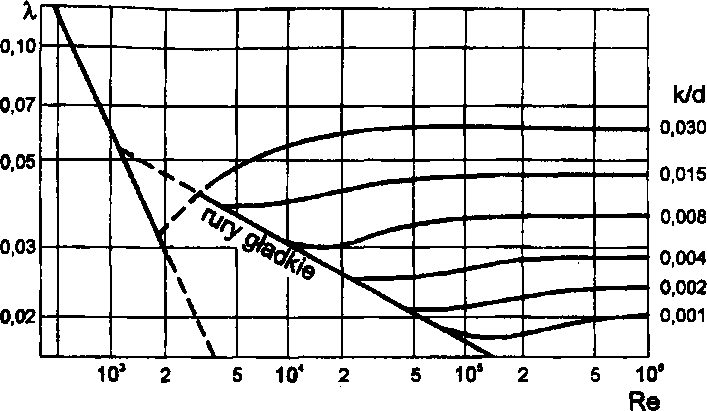
Rys. 4.1 Współczynnik oporów przepływu w przewodach o różnym stopniu szorstkości

ścianek

Opory miejscowe są związane z lokalnymi zmianami prędkości i kierunku przepływu wywołanymi przez elementy armatury i inne elementy zainstalowane na rurociągu. Wielkość oporu miejscowego (np. spowodowanego przez zainstalowany .na rurze zawór, kolanko, zwężkę, itp.) jest proporcjonalna do energii kinetycznej płynu. Strata ciśnienia spowodowana przez opór miejscowy może być wyrażona równaniem

Ap„ = P    (4.7)

w którym ę jest współczynnikiem oporu miejscowego dla danego rodzaju elementu armatury.

Strata ciśnienia wywołana oporem miejscowym może być także obliczona w oparciu o tzw. długość zastępczą L_e

Ap_m = ^y^p    (48)

Jak widać z powyższego równania, L_e jest długością prostego odcinka rury, w którym strata ciśnienia na skutek oporów tarcia jest taka sama jak strata ciśnienia na skutek oporu miejscowego.

Z porównania dwóch ostatnich zależności wynika, że