img060

Jest to tak zwany test dla par danych. Wykorzystujemy w nim statystykę t

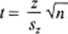
gdzie:

(5.12)

z — wartość średnia różnic z_h

s_z — oszacowanie odchylenia standardowego różnic według znanego wzoru

•s,

'z

(5.13)

Statystyka (5.12) ma rozkład / o n- 1 stopniach swobody. Dalsze postępowanie znamy. Korzyścią ze stosowania tego testu jest wyeliminowanie wpływu różnic między poszczególnymi obiektami (np różnic osobniczych między pacjentami), dlatego też wynik testu można uważać za bardziej obiektywny.

Jeżeli tylko są możliwości, należy stosować test dla par. a nie poprzednio omówiony test porównywania dwóch średnich. Jeżeli jednak musimy porównywać dwie średnie, a dodatkowym utrudnieniem jest niemożność przyjęcia założenia o równości wariancji w obu populacjach (por. punkt 5.7), z których wylosowano próby, to gdy obie próby mają dużą liczebność (/i₁, n₂> 100) można wykorzystywać statystykę u

u

(5.14)

(oznaczenia jak we wzorach (5.9) i (5.10)) mającą w przybliżeniu rozkład normalny standaryzowany. Jeżeli zaś dysponujemy małymi próbami lub próby znacznie różnią się liczebnością, to lepiej stosować statystykę /:

t

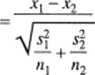
(5.15)

która ma w przybliżeniu rozkład f-Studenta o liczbie stopni swobody v danej wzorem

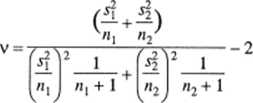
(5.16)

60